
Zum gewünschten Abschnitt springen und mit ALT ← wieder hierher zum Inhaltsverzeichnis zuück.
Dies ist "Work in Progress". Die Informationen zu den grau gestellten Abschnitten liegen vor und werden Schritt für Schritt eingegeben.
2 Grundlagen
2.1 Einordnung
2.2 Bestandteile einer PV-Anlage – Vokabeln und Definitionen
2.3 Formelzeichen
2.4 Geneigte Fläche und Sonnenstand
2.5 Globalstrahlung
2.6 Globalstrahlung auf die geneigte Fläche
Anteil der direkten Strahlung
Anteil der diffusen Strahlung
Anteil der reflektierten Strahlung
Gesamte Strahlung auf die geneigte Fläche
Mehr zum Diffusanteil
2.7 Strahlungssumme mit Klimaeinflüssen
Strahlungssummen aus dem Global Solar Atlas (GSA)
Strahlungssummen aus dem Photovoltaic Geographical Information System (PVGIS)
2.8 Umrechnung der Strahlungssumme zur horizontalen Fläche auf die Strahlungssumme zur geneigten Fläche
2.9 Von der Strahlung zum Ertrag
Standardtestbedingungen und Nennleistung
Spezifischer Ertrag
Volllaststunden
2.10 Wirkungsgrade in einer langen Kette
Wirkungsgradkette – Prinzipdarstellung
Wirkungsgradkette – Photovoltaik
2.11 Wirkungsgrad zum geographischen Ort
Standard-Wirkungsgrad zum geographischen Ort
Alternativ-Wirkungsgrad zum geographischen Ort
2.12 Wirkungsgrad zur Ausrichtung der Module
Standard-Wirkungsgrad zur Ausrichtung der Module
Alternativ-Wirkungsgrad zur Ausrichtung der Module
2.13 Wirkungsgrade zum Solarmodul
Modulwirkungsgrad bei Standardtestbedingungen
Temperatur- und Globalstrahlungswirkungsgrad
Wirkungsgrad zur Berücksichtigung verschiedener Verluste am Solargenerator
2.14 Wirkungsgrade zum Wechselrichter
Wechselrichter-Umwandlungswirkungsgrad
Wirkungsgrad zur Berücksichtigung verschiedener Verluste am Wechselrichter
2.15 Wirkungsgrade zum System
Wirkungsgrad zur Berücksichtigung verschiedener Verluste von Komponenten im System
Verfügbarkeit
2.16 Performance Ratio (PR) als Wirkungsgrad
2.17 Typische Wirkungsgrade
2.18 Rechnen mit Wirkungsgraden
2.19 Charakteristische Parameter
Fläche der Module
Nennleistung der PV-Anlage
Nennleistung des Wechselrichters am Ausgang
Phasenverschiebung und Wirkfaktor
Nennleistung des Wechselrichters am Eingang
Dimensionierungsfaktor und andere Nennleistungsverhältnisse
Energienutzungsfaktor
Schieflast
CO2-Reduktion
Darstellung charakteristischer Parameter am Beispiel einer PV-Planungssoftware
3 Ergänzungen
3.1 Systematik der Strahlung
Absorption, Reflexion und Transmission
Optische Dicke
Optische Luftmasse (Air Mass) und optische Dicke der Atmosphäre
3.2 Berechnung der Modultemperatur
3.3 Berechnung der Wechselrichterkennlinie aus maximalem und EU-Wirkungsgrad
3.4 Mehr Sonnenscheinstunden und Solarstrahlung durch Klimawandel
3.5 Optimale Ausrichtung der Module: optimaler Neigungswinkel, βopt, optimaler Azimut, γopt
3.6 Historische Berechnung der Strahlungssumme, H auf eine horizontale Fläche mit Klimaeinflüssen
4 PV-Planungssoftware
4.1 Gliederung
4.2 Kostenlos von Firmen und Organisationen
4.3 Kostenlos von Hochschulen
4.4 Mehr kostenlos (aber noch nicht getestet von mir)
4.5 Kommerzielle Tools
4.6 Literatur über PV Planungssoftware
5 Visualisierung, Überwachung und Monitoring
5.1 Motivation
5.2 Visualisierung von PV-Daten
5.3 Überwachung versus Monitoring
5.4 Sechs Möglichkeiten zur Bewertung von Anlagendaten und Leistungsparametern
5.5 Zu 4.: Monitoring durch Vergleich des spezifischen Ertrags aus einer Ertragsdatenbank
5.6 Zu 5.: Monitoring basierend auf der Solarstrahlung vom DWD
5.7 Zu 6.: Monitoring durch Berechnung der Globalstrahlung an einem wolkenlosen Tag
Monitoringkonzept 6: Darstellung an einer konkreten PV-Anlage
Monitoringkonzept 6: Verallgemeinerung
6 Betriebsarten von PV-Anlagen
7 Eigenverbrauch und Überschusseinspeisung
8 Einnahmen und Ausgaben
9 Investitionsrechnung und Auswahlstrategien
10 Investieren in Photovoltaik
11 Bürgerbeteiligung an der Energiewende
12 Bürgersolargenossenschaften
6.1 Volleinspeisung
6.2 Eigenverbrauch und Überschusseinspeisung
6.3 Anlagensplitting
6.4 Inselbetrieb
7.1 Einleitung
7.2 Grundlagen
7.3 Jahresstromverbrauch
7.4 Eigenverbrauchsanteil aus maximalem Autarkiegrad
Maximaler Autarkiegrad aus der Zählerablesung
Maximaler Autarkiegrad aus der Jahresdauerlinie
7.5 Eigenverbrauchsanteil aus Standardlastprofilen
7.6 Eigenverbrauchsanteil aus Lastgängen
7.7 Batteriespeicher
7.8 Eigenverbrauchsanteil mit Batteriespeicher
8.1 Einspeisevergütung
8.2 Ersparnis durch Eigenverbrauch
8.3 Mieteinnahmen aus einer PV-Anlage
8.4 Anschaffungskosten der PV-Anlage und Abschreibung
8.5 Laufende Kosten
Versicherungen
Dachmiete
Reparaturen
8.6 Entsorgung und Restwert
8.7 Gewinn und Verlust
8.8 Steuern
9.1 Statische und dynamische Verfahren der Investitionsrechnung
9.2 Kapitalwertmethode (NPV)
9.3 Modifikationen des NPV
9.4 Vermögensmethode (NFV)
9.5 Methode des internen Zinsfußes (IRR) (IRR aus NPV versus NFV)
9.6 Problem der Wiederanlage
9.7 Modifikationen der IRR
9.8 Annuitätenmethode (EAC)
9.9 Amortisationsrechnung (BEP)
9.10 Stromgestehungskosten (LCOE)
9.11 Nutzwertanalyse – Kombination finanzieller und nicht-finanzieller Kriterien
Methoden zur Bestimmung der Gewichtungsfaktoren
Methoden zur Quantifizierung der Kriterien
Beispiel zur Nutzwertanalyse
10.1 Balkonanlage
10.2 Dachanlage
10.3 Solargenossenschaft
10.4 Solarfonds
10.5 Solarkapitalmarkt: Aktien, ETFs, Anleihen
11.1 Idee und Umsetzung
11.2 Aktivitäten: Photovoltaik, Windenergie, Blockheizkraftwerk, energetische Sanierung
11.3 Rechtsformen: GBR, e.V., Genossenschaft, gGmbH, GmbH, AG
...
Anhang
Anhang A DVD: Photovoltaische Anlagen (Passwort erforderlich)
Anhang B PDFs im Entwurfsstadium
Diesen Fragen soll am Ende nachgegangen werden in Abschnitten wie "Investieren in Photovoltaik", "Bürgerbeteiligung an der Energiewende" oder "Bürgersolargenossenschaften".
Zunächst geht es um das Handwerkzeug zum Planen von PV-Anlagen. Dabei kann so gegliedert werden:
Im Systems Engineering Handbook in Abschnitt 4.4.1.2 "Process Activities" (PDF-Seite 74) wird die "Doctrine of Successive Refinement" beschrieben.
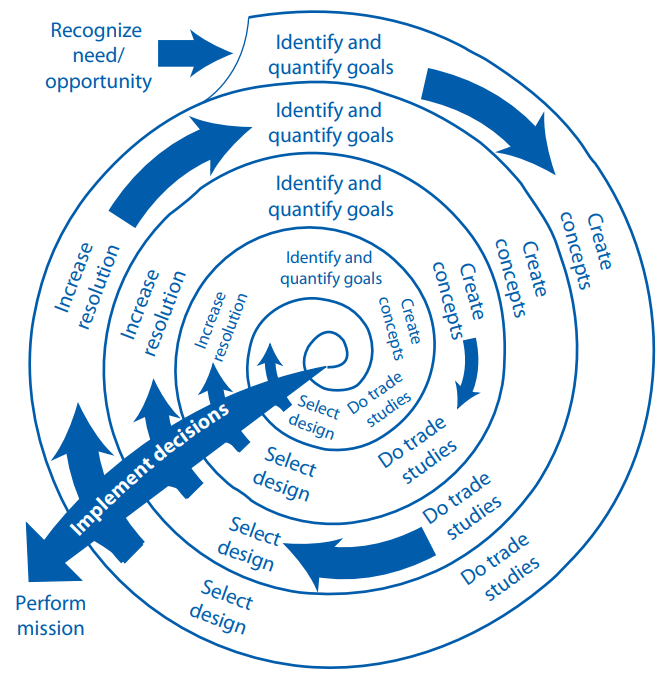
NASA's doctrine of successive refinement.
|
NASA's Doctrine of Successive Refinement
The realization of a system over its life cycle involves a succession of decisions among alternative courses of action. If the alternatives are precisely defined and thoroughly understood to be well differentiated in the cost-effectiveness space, then the systems engineer can make choices among them with confidence.
Identify and Quantify Goals
Define Alternative Design Solutions
Analyze Each Alternative Design Solution
Select the Best Design Solution Alternative
Increase the Resolution of the Design |
Sinnvoll ist eine Abgrenzung des Themas mit einer Definition:
|
Definition: Planen von Photovoltaikanlagen
Unter "Planen von Photovoltaikanlagen" werden hier die Aktivitäten verstanden, die erforderlich sind, um eine optimale Konfiguration der PV-Anlage zu finden, eine optimale Größe der Anlage, sowie eine Auswahl geeigneter Hauptkomponenten (Solarmodul, Wechselrichter, ...). Das erfordert auch grundsätzliche Überlegung zur Unterkonstruktion einschließlich dessen Verankerung. Das Zusammenspiel der Hauptkomponenten miteinander sollte verstanden werden. Es wird jedoch davon ausgegangen, dass die PV-Anlage von einem Installateur errichtet wird, der verantwortlich ist für die Details der Anlagenauslegung und den Anlagenbau bis hin zum elektrischen Anschluss an das Netz. Komponenten werden eingekauft (nicht ausgelegt) und eingebaut. Grundlegende Kenntnisse über die Komponenten sind erforderlich, insbesondere ein Verständnis der Datenblätter, nach denen die Integration der Komponenten in das Gesamtsystem erfolgt. Der spätere Betrieb (Anlagenmonitoring) muss in der Planung berücksichtigt werden, weil verschiedene Monitoringkonzepte entsprechende Sensoren und Anzeigen benötigen. |
Zunächst geht es daher um diese Fragen:
Diese Seite mag hilfreich sein für Solar- und Klimagruppen, um ein gemeinsames Verständnis über das Handwerkzeug zur Planung von PV-Anlagen zu erlangen.
Die Seite wendet sich ebenfalls an Studierende im Ingenieurwesen sowie an alle "Schatzsucher" im WWW.
Nicht zuletzt hilft mir die Seite, meine eigenen Gedanken zu strukturieren.
Wer eine praktische und fundierte Anleitung für Einsteiger zum Thema "PV" sucht, dem sei der
Solarbrief 01/2023 vom
Solarenergie-Förderverein Deutschland e.V. empfohlen.
Er enthält auf 86 Seiten
 Das kleine Solaranlagen 1x1 (Link startet Download)
(Archiv) *.
Das kleine Solaranlagen 1x1 (Link startet Download)
(Archiv) *.
* Um diese Seite zukunftssicher zu halten, benutze ich perma.cc der Harvard Law School Library. Ein Perma-Link ist ein zuverlässiger, permanenter Link zu einer unveränderlichen Aufzeichnung. Mehr dazu von Wikipedia. Aber nicht jeder externe Link ist hier archiviert – das wäre auch unpraktisch. Perma.cc speichert Webseiten im WARC-Format. Leider wird dieses Standardformat nicht von allen Browsern fehlerfrei zurückgelesen. Ich nutze Microsoft Edge. Mit diesem Browser wird perma.cc (nach meiner Beobachtung) korrekt angezeigt.
Ziel
Hier soll es um die Grundlagen der Photovoltaik gehen, aber mit etwas mehr Eindringtiefe als anderswo im WWW üblich.
U.a. folgende Fragen sollen beantwortet werden:



Gliederung und Vorgehen
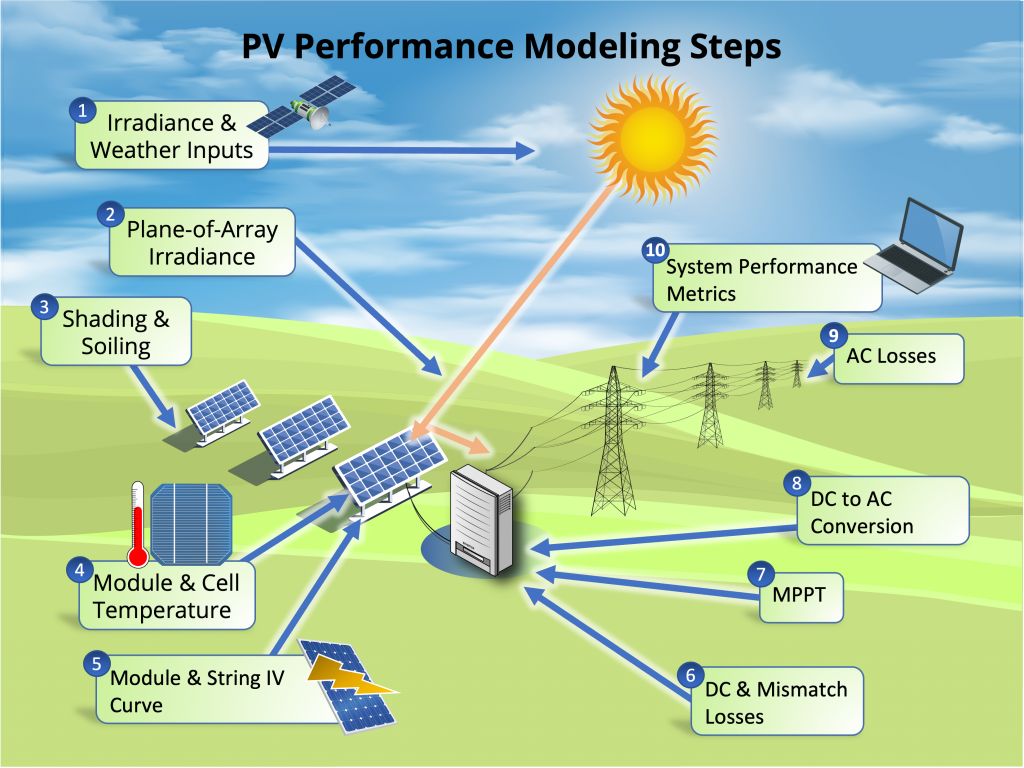
PV Performance Modeling Steps. Sandia National Laboratories, https://pvpmc.sandia.gov.
Im Unterschied zum alphabetischen Glossar folgt dieser Text den Parametern durch die Logik der PV-Anlage und beginnt – ähnlich, wie im Bild – mit der Solarstrahlung auf eine geneigte Fläche. Vorher verständigen wir uns aber noch über die Definition wichtiger Begriffe in der Photovoltaik, damit klar ist, was eigentlich gemeint ist. Weiterhin werden wichtige Formelzeichen in einer Systematik zusammengestellt.
Meine wichtigste Quelle zur Berechnung der Solarstrahlung
DUFFIE, John A., BECKMAN, William A., 2013. Solar Engineering of Thermal Processes. New York: John Wiley.
Available from: https://doi.org/10.1002/9781118671603,
archived at: https://perma.cc/968F-P8YD *,
PDF-1980 of Ch. 1.1-1.6, 2.8  . .
|
Die Bestandteile einer klassischen netzgekoppelten Photovoltaikanlage sind im Bild gezeigt. Weitere Bestandteile (Stromspeicher, ...) sind möglich bei einer Anlage mit Eigenverbrauch. Hier geht es erst einmal um die systematische Wortwahl.
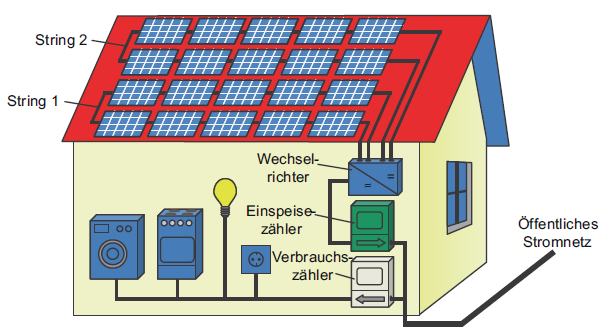
Aufbau einer klassischen netzgekoppelten Photovoltaikanlage.
Quelle: K. Mertens, www.lehrbuch-photovoltaik.de, Bild 1.10.
| Deutsch | Englisch | Definition |
|
Photovoltaikanlage PV-Anlage Solaranlage Solarstromanlage |
photovoltaic system PV system solar systems solar power system |
Anlage zur Erzeugung elektrischer Energie aus Sonnenlicht bestehend aus einem Solargenerator, Verkabelung, Wechelrichter, Stromzähler und weiteren Komponenten je nach Typ und Betriebsart der Anlage. |
|
Solargenerator Photovoltaikgenerator PV-Generator |
solar array photovoltaic array PV array |
Alle Solarmodule einer PV-Anlage und deren Gleichstromverkabelung. Der Solargenerator besteht aus einem oder mehreren Strängen. |
| Strang | string | Mehrere in Reihe geschaltete Solarmodule. |
|
Solarmodul Photovoltaikmodul PV-Modul Solarpanel |
solar module photovoltaic module PV module solar panel |
Das Solarmodul besteht aus Solarzellen, die in Reihe geschaltet sind (Zellverstringung). Aufbau des Solarmoduls (von oben nach unten): Glasscheibe, transparente Kunststoffschicht, Solarzelle elektrisch miteinander verschaltet, Kunststofffolie zum Verkleben der Rückseite, Rückseite mit einer witterungsfesten Kunststoffverbundfolie oder einer weiteren Glasscheibe (sogenannte Glas-Glas-Module) Anschlussdose mit Bypassdioden, Aluminiumprofil-Rahmen zum Schutz und zur Befestigung des Verbundes. |
|
Solarzelle photovoltaische Zelle PV Zelle |
solar cell photovoltaic cell PV cell |
Ein elektrisches Bauelement, das Sonnenlicht, direkt in elektrische Energie umwandelt. Die physikalische Grundlage der Umwandlung ist der photovoltaische Effekt. |
| Unterkonstruktion | substructure | Die Unterkonstruktion verbindet die Solarmodule mit dem Untergrund (Boden, Dach, ...) und richtet die Module idealerweise so aus, dass der höchstmögliche Jahresertrag oder der höchstmögliche Eigenverbrauch über das Jahr gewährleistet wird. |
| Wechselrichter | inverter | Ein Solarwechselrichter besitzt auf der Eingangsseite einen oder mehrere Maximum-Power-Point-Tracker (Mikroprozessor mit MPPT-Algorithmus), die dafür sorgen, dass die elektrische Belastung des jeweiligen Strangs so angepasst wird, dass dem Strang die größte mögliche Leistung entnommen wird. Auf der Ausgangsseite befindet sich ein ein- oder dreiphasiger Wechselrichter, der die Gleichspannung in Wechselspannung umwandelt sich automatisch mit dem Stromnetz synchronisiert. |
| Verkabelung | cabling | Elektrische Verbindung der Komponenten der PV-Anlage. |
|
Stromspeicher Batterie |
power storage system battery |
Elektrochemisches Gerät bestehend aus mehreren Zellen zur Aufnahmen, Speicherung und Abgabe elektrischer Energie. |
|
Stromzähler Zähler |
electric meter meter |
Ein Messgerät, das die übertragene elektrische Energie an einem Zählerpunkt erfasst. Bei PV-Anlagen wird unterschieden: Bezugszähler, Einspeisezähler, Zweirichtungszähler und Ertragszähler. |
| Hausanschlusskasten | house connection box | Ein vom Netzbetreiber geforderter Kasten, mit dem ein Haus an das öffentliche Stromnetz angeschlossen wird und sich im Hausanschlussraum befindet. Der Hausanschlusskasten ist die Übergabestelle vom Verteilungsnetz. |
| Anlagenüberwachung | plant monitoring | Das Monitoring von PV-Anlagen ermöglicht es Betreibern, schnell auf Störungen zu reagieren und Ertragsverluste zu vermeiden. |
| Das ist etwas anderes: | ||
|
Solargenerator Gleiche Bezeichnung wie oben, aber andere Bedeutung! |
solar generator solar power generator |
Ein Solargenerator ist die Kombination von tragbaren Solarmodulen, Batterie, Batterieladegerät und Wechselrichter in einem einzigen Gerät, mit dem Sonnenenergie aufgenommen, gespeichert und verteilt werden kann. Solargeneratoren werden für Camping, Wohnmobil und als Notstromgenerator genutzt. |
| Notstromgenerator | emergency generator | Ein Notstromaggregat ist ein Gerät zur Stromerzeugung, das bei Ausfall der regulären Stromversorgung eingesetzt wird. |
Diese Darstellung richtet sich nach DIN 1304 ("Formelzeichen") bzw. nach ISO/IEC 80000 ("Quantities and Units"). Die Normen sind nicht frei zugänglich. Stattdessen gibt es entsprechende Informationen bei Wikipedia. Daraus werden für die Photovoltaik die wichtigsten Formelzeichen extrahiert. Dies geschieht auch im Vergleich mit ISO 9488 Solar Energy – Vocabulary. Wo immer hilfreich, wurden die allgemeinen Formelzeichen (ISO/IEC 80000) an ISO 9488 und den Sprachgebrauch in der Solarbranche angepasst.
Angegeben sind der Name des Parameters auf Deutsch (auf Englisch), der Name der Einheit ausgeschrieben (und in der Abkürzung) und evtl. noch eine Berechnungsgleichung für den Parameter und eine Umrechnung der Einheiten.
Hinweis: Angaben in Prozent sind so zu verstehen (Beispiel): 5 % = 5/100 = 0,05. Daher wird in Gleichungen nicht zwischen 5 % und 0,05 unterschieden.
Masse (mass), m, Kilogramm (kg) Länge (length), l, Meter (m) Zeit, (time), t, Sekunde (s) Temperatur (temperature), T, Kelvin (K) ebener Winkel (plane angle), α, β, γ, ..., Grad (°, deg) Drehwinkel (Rotation), ϕ, θ, ..., Grad (°, deg) Fläche, Flächeninhalt, Oberfläche, Querschnittsfläche (area), A, Quadratmeter (m2) AG ist die Brutto-Kollektorfläche (gross collector area) des Moduls (ISO 9488). Das ist die grösste projizierte Fläche eines vollständigen Kollektors, ohne Vorrichtungen für die Befestigung. Volumen (volume), V, m3 Dichte (density), ρ, ρ = m/V, kg/m3 Kraft (force), F, Newton (N), 1 N = 1 kg·m/s2 Energie, (energy), E, Joule (J), 1 J = 1 Nm = 1 Ws Leistung, (power), P, Watt (W), 1 W = 1 J/s = 1 Nm/s = 1 kg·m2/s2 Wirkungsgrad (energy conversion efficiency), η = Pout / Pin = Eout / Ein (dimensionslos) elektrische Stromstärke (electric current), I, Ampere (A) elektrische Spannung (voltage), U, Volt (V) In Gleichstromnetzen (in direct current (DC) systems): elektrische Leistung (electrical power), P, P = U·I, Watt (W), 1 W = 1 V·A, elektrischer Widerstand (electrical resistance), R, Ohm (Ω), R = U / I, 1 Ω = 1 V/A, In Wechselstromnetzen (in alternating current (AC) systems): Wirkleistung (active power), P, Watt (W) Blindleistung (reactive power), Q, var Scheinleistung (complex power), S, VA |
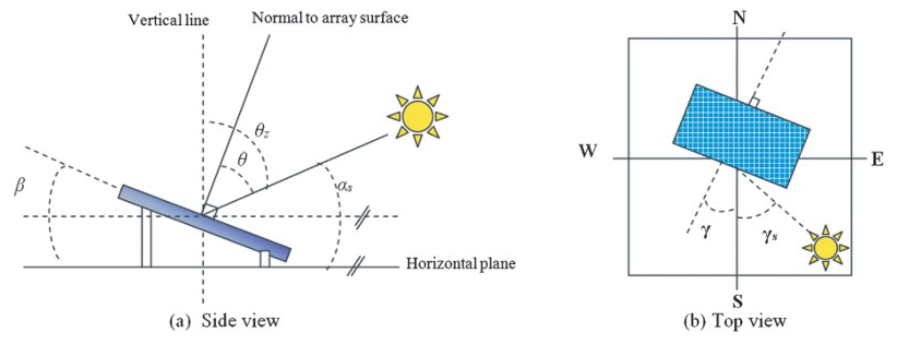
Winkel an einer geneigten Fläche.
Nach: Al-Messabi et al., CC-BY, https://doi.org/10.1080/21642583.2016.1228485
Die geneigte Fläche ist gekennzeichnet durch:
Wenn die Sonne genau im Süden steht (ω = 0) und der Solargenerator nach Süden ausgerichtet ist (γ = 0), dann erhalten wir direkt oder mit Gleichung (1) von unten:
Wenn die Sonne genau im Süden steht (ω = 0), dann erhalten wir mit einem Additionstheorem für die cos-Funktion die Gleichung (1):
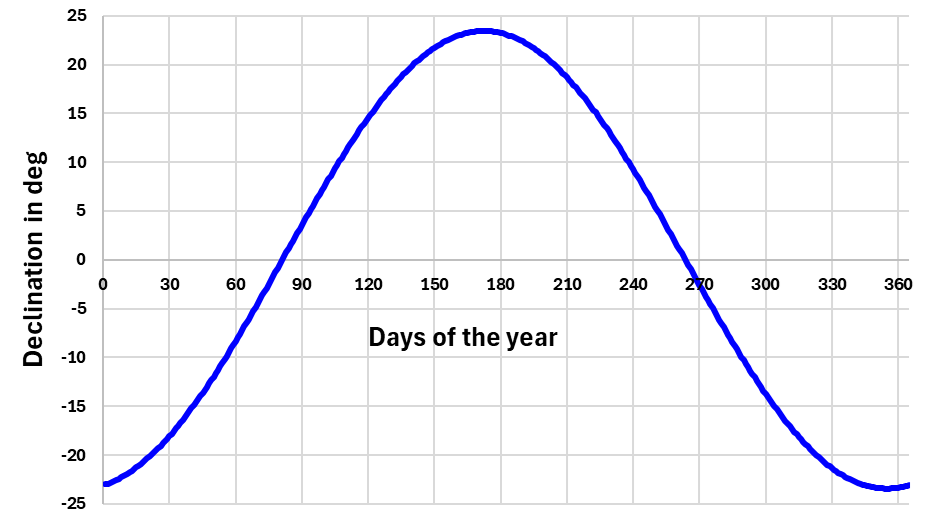
Deklination, δ
23,44° ist die
Schiefe der Ekliptik.
Die "10" im Term (n+10) ist die Anzahl der Tage von der
Wintersonnenwende
(21.12.) bis zum Anfang des Jahres.
Genauere Gleichungen für δ gibt es hier.
Globalstrahlung (global radiation, total solar radiation, irradiance), G in W/m2 (Leistung pro Fläche) ist die gesamte auf die horizontale Erdoberfläche auftreffende Solarstrahlung. Vereinbarung: Die Globalstrahlung, G ohne einen Index bezieht sich immer auf eine horizontale Fläche. Die Globalstrahlung ist die Summe aus Direkt- und Diffusstrahlung.
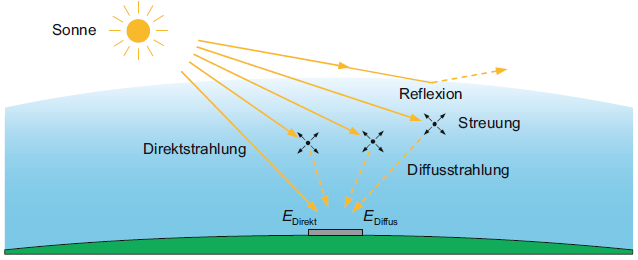
Die Globalstrahlung ist die Summe aus Direkt- und Diffusstrahlung.
Quelle: K. Mertens, www.lehrbuch-photovoltaik.de, Bild 2.4.
Außerhalb der Atmosphäre wirkt die extraterrestrische Sonnenstrahlung (extra-terrestrial solar radiation). Die Solarkonstante (solar constant), Gsc ist die Bestrahlungsstärke der Sonnenstrahlung außerhalb der Erdatmosphäre auf eine Ebene senkrecht zur Einstrahlungsrichtung, wenn die Erde sich in ihren mittleren Abstand zur Sonne befindet (149,5·106 km). Die Solarkonstante beträgt
Die Solarkonstante Gsc,n an einem bestimmten Tag des Jahres, n ist abhängig von der Entfernung der Erde zur Sonne. Die Erde erreicht die größte Sonnennähe in den ersten Tagen des Januars eines jeden Jahres. Daher ist (Duffie 1980, Gl. 1.4.1)
Die extraterrestrische Bestrahlungsstärke auf eine horizontale Ebene außerhalb der Erdatmosphäre (extra-terrestrial irradiance on a horizontal plane above the Earth's atmosphere), G0 kann für einen Punkt oberhalb der Erde, auf einer bestimmten geographischen Breite, an einem bestimmten Tag im Jahr und zu einer bestimmten Uhrzeit berechnet werden (Duffie 1980, Gl. 1.8.1).
Mit dem atmosphärischen Transmissionsfaktor (clearness index), k kann die Bestrahlungsstärke auf einer horizontalen Ebene am Boden berechnet werden. Die Schwierigkeit liegt in der Bestimmung von k. Bei klarem Himmel beträgt der Transmissionsfaktor etwa 0,8. Ein Transmissionsfaktor von weniger als 0,2 deutet auf einen bedeckten Himmel mit optisch ziemlich dicken Wolken hin. Bei 0,3 < k < 0,6, hat die Wolkendecke eine geringe optische Dicke (optical depth) oder kann aus fragmentierten Wolken mit ziemlich großer optischer Dicke bestehen.
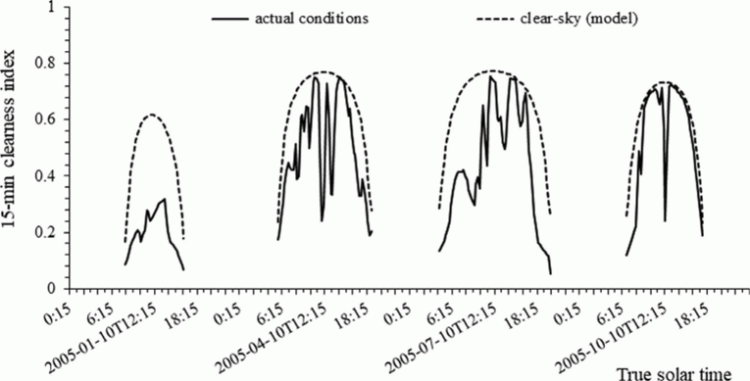
Der Transmissionsfaktor (clearness index), k = G / G0 für drei ausgewählte Tage.
Standort auf 50° nördlicher Breite.
Es werden zwei Profile des Transmissionsfaktors dargestellt: das tatsächliche Profil und
das Profil unter der Annahme eines wolkenlosen Himmels (clear sky).
Datenquelle: HelioClim-3-Datenbank und McClear-Modell.
Quelle: WALD, Lucien, 2021. Fundamentals of Solar Radiation. https://doi.org/10.1201/9781003155454-6.
Auszug: Clearness Index Definition.
Ebenso kann mit dem atmosphärischen Transmissionsfaktor (clearness index), k die Bestrahlungsstärke auf einer Ebene senkrecht (normal) zur Einstrahlung am Boden berechnet werden.
Der Transmissionsfaktor (clearness index), k wird in der Physik allgemein als Transmissionsgrad (transmittance), T bezeichnet (siehe etwas weiter unten).

Globalstrahlung Gn auf eine Fläche senkrecht (normal) zur Sonne, mittags in Deutschland.
Daraus kann auch k = Gn / Gsc abgeschätzt werden.
Werte für den Sommer (in Klammern für den Winter):
klarer Himmel: k = 0,74 (0,37);
leichte bis mittlere Bewölkung: k = 0,44 (0,22);
starke Bewölkung: k = 0,22 (0,11).
Quelle: Solar Power, 2015
und Wikipedia.
Wir merken uns: Bei hohem Sonnenstand und klarem Himmel erreicht die Globalstrahlung auf eine senkrechte Fläche (in Deutschland) maximal Gn = 1000 W/m2.
Unterschieden und weiter differenziert wird hinsichtlich der Art der Strahlung und der Ausrichtung der Fläche:
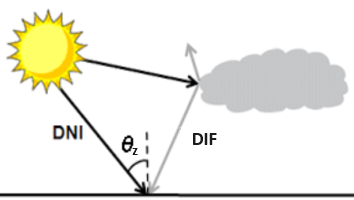
Anmerkung: Die Abkürzungen GHI, DHI, DIF und DNI werden sowohl für die Globalstrahlung (irradiance) wie auch für die Strahlungssumme (irradiation) genutzt.
GHI = DHI + DIF DHI = DNI * cos θz GHI = DNI * cos θz + DIF
Gegenben ist online i.d.R. nur GHI, DHI und DNI. DIF muss dann berechnet werden mit DIF = GHI - DHI .
Die Globalstrahlung an einem wolkenlosen Tag (clear sky radiation), Gc (mit einer Sichtweite von 23 km) kann berechnet werden zu jeder Zeit des Tages aus der Summe von Direktstrahlung und Diffusstrahlung.
Zur Berechnung der Globalstrahlung an einem wolkenlosen Tag auf eine horizontale Fläche, Gc ist ein Excel-Programm nach Duffie (1980, Ch. 2.8) vorhanden (Download auf Nachfrage). Die Lösung ist Teil der Berechnung für die geneigte Fläche (s.u.).
Die Werte der Globalstrahlung an einem wolkenlosen Tag können zu Monatssummen oder Jahressummen (s.u.) addiert werden. Das ist aber wenig hilfreich für die Praxis, weil die Klimaeinflüsse (Wolken) ebenfalls berücksichtigt werden müssen.
Im Abschnitt zur Globalstrahlung, G gab es für die horizontale Fläche nur zwei Anteile, die Direktstrahlung (beam radiation), Gb und die Diffusstrahlung (diffuse radiation), Gd. Es gibt aber noch einen weiteren Strahlungsanteil. Dies ist die reflektierte Strahlung aus der Umgebung, insbesondere vom Boden (reflected radiation from the surroundings, especially from the ground), Gr . Die Strahlung vom Boden kann die horizontale Fläche nicht erreichen, jedoch die geneigte Fläche. Die Globalstrahlung auf die geneigte (tilted) Fläche, Gt ist die Summe der genannten Anteile.
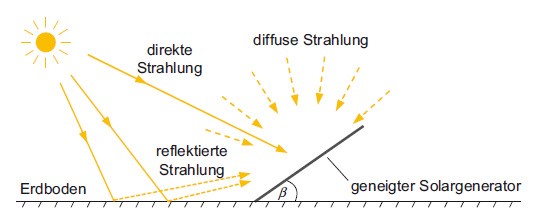
Strahlungssituation bei geneigter Fläche. Die Strahlung setzt sich zusammen aus direkter, diffuser und reflektierter Strahlung.
Quelle: K. Mertens, www.lehrbuch-photovoltaik.de, Bild 2.14.
Anteil der direkten Strahlung
Im Bild unten ist der Anteil der direkten Strahlung auf verschiedene Flächen gezeigt.
Auf die Flächen Asenkrecht, AGen und AH fällt immer die gleiche Strahlung
– nur mehr oder weniger auf die jeweilige Fläche verteilt, je nach deren Größe.
Das sieht man daran, dass die Sonnenstrahlen im Bild einen größeren Abstand haben (AH) oder einen kleineren (Asenkrecht).
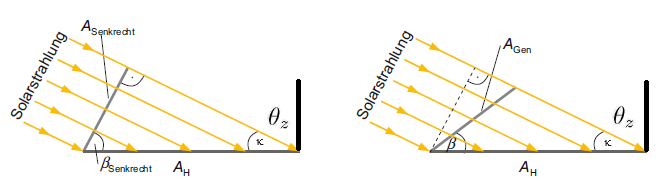 Einfluss der Solargeneratorneigung auf die direkte Strahlung.
A ist die jeweilige Fläche.
Einfluss der Solargeneratorneigung auf die direkte Strahlung.
A ist die jeweilige Fläche.
Nach: K. Mertens, www.lehrbuch-photovoltaik.de, Bild 2.15.
Linkes Bild – Vergleich horizontale Fläche mit senkrechter Fläche:
βsenkrecht ist der Winkel zwischen der horizontalen Fläche und der senkrecht bestrahlten Fläche.
βsenkrecht = θz (Winkelsumme im rechten Winkel. Winkelsumme im Dreieck).
Asenkrecht = AH cos θz
; Asenkrecht / AH = cos θz
; AH = Asenkrecht / cos θz .
Eine große Fläche bedeutet bei gegebenem Strahlungsangebot eine geringe Leistung pro Fläche.
Daher ist Gb / Gb,n = Asenkrecht / AH und
Gb = Gb,n cos θz
(das wurde im Abschnitt Globalstrahlung schon angegeben, aber erst hier hergeleitet).
Rechtes Bild – Vergleich Generatorfläche mit senkrechter Fläche:
Der neue Winkel βsenkrecht ist der Winkel zwischen der Generatorfläche und der senkrecht bestrahlten Fläche. Dieser neue Winkel ist θ . Das gilt allgemein.
Hier im Bild ist die Generatorfläche zur Sonne ausgerichtet. Es gilt: Der neue Winkel βsenkrecht ist um β verkleinert:
θ = θz - β (das geht auch hervor aus dem Bild im Abschnitt Geneigte Fläche).
Asenkrecht = AGen cos θ
; Asenkrecht / AGen = cos θ
; AGen = Asenkrecht / cos θ .
Eine große Fläche bedeutet bei gegebenem Strahlungsangebot eine geringe Leistung pro Fläche. Daher ist
Gb,t / Gb = AH / AGen
Jetzt werden die Ausdrücke für die Flächen eingesetzt. Damit ist
|
Aufgabe
Ein Solargenerator steht auf einer geographischen Breite von ϕ = 50°, ist nach Süden ausgerichtet und hat eine Neigung von β = 35°. Zu berechnen ist das Verhältnis der Direktstrahlung auf die geneigte Fläche, Gb,t zur Direktstrahlung auf die horizontale Fläche, Gb, also das Verhältnis Rb am Mittag des 16.05. eines Jahres. Lösung: Der 16.05. ist der 136. Tag im Jahr (einfach zu ermitteln mit Duffie, 1980, Tabelle 1.6.1). Die Deklination am 16.05. ist δ = 19° (Diagramm oder Gleichung). An diesem Tag steht die Sonne mittags am Äquator nicht senkrecht, sondern um θz, Äquator = 19° nach Norden. Weiter im Norden auf ϕ = 50° steht die Sonne im Süden und 50° tiefer. Also
θz = 50° - 19° = 31°. Jetzt wird die Fläche um 35° der Sonne entgegen geneigt, so dass diese senkrechter (mit kleinerem Winkel) auf die Fläche scheinen kann.
Es ist also θ = 31° - 35°; = -4°. Rb = cos 4° / cos 31° = 1,16. Antwort: Die Direktstrahlung ist um den Faktor 1,16 auf der Fläche höher als auf der (horizontalen) Erdoberfläche. Für den (wichtigen) Spezialfall, dass die Generatorfläche nach Süden ausgerichtet ist und die Sonne auch gerade im Süden steht, erhalten wir einfache Gleichungen für θ und für θz. Diese Gleichungen wurden im Abschnitt Geneigte Fläche und Sonnenstand schon hergeleitet aus der allgemeinen (sehr langen) Gleichung für θ und hier durch eine einfache Herleitung am Spezialfall bestätigt. |
Anteil der diffusen Strahlung
Der Anteil der diffusen Strahlung an der Gesamtstrahlung, der Diffusanteil (diffuse/global ratio), Gd / G
hängt ab vom Wetter und vom Sonnenstand.
Der Dissusanteil kann für jede Zeit eines klaren Tages berechnet werden. Beispiel: 0,14 Hamburg, mittags, Juli.
An einem bewölkten Tag ist der Diffusanteil höher, aber ohne Messwerte unbekannt.
Der Diffusanteil ergibt sich aber zusammen mit einer Wetterstatistik gemittelt für einen Monat.
In Deutschland haben die Monate Dezember und Januar einen hohen Diffusanteil (0,7 bis 0,8).
Die Monate April und Mai haben einen geringen Diffusanteil (0,35 bis 0,45).
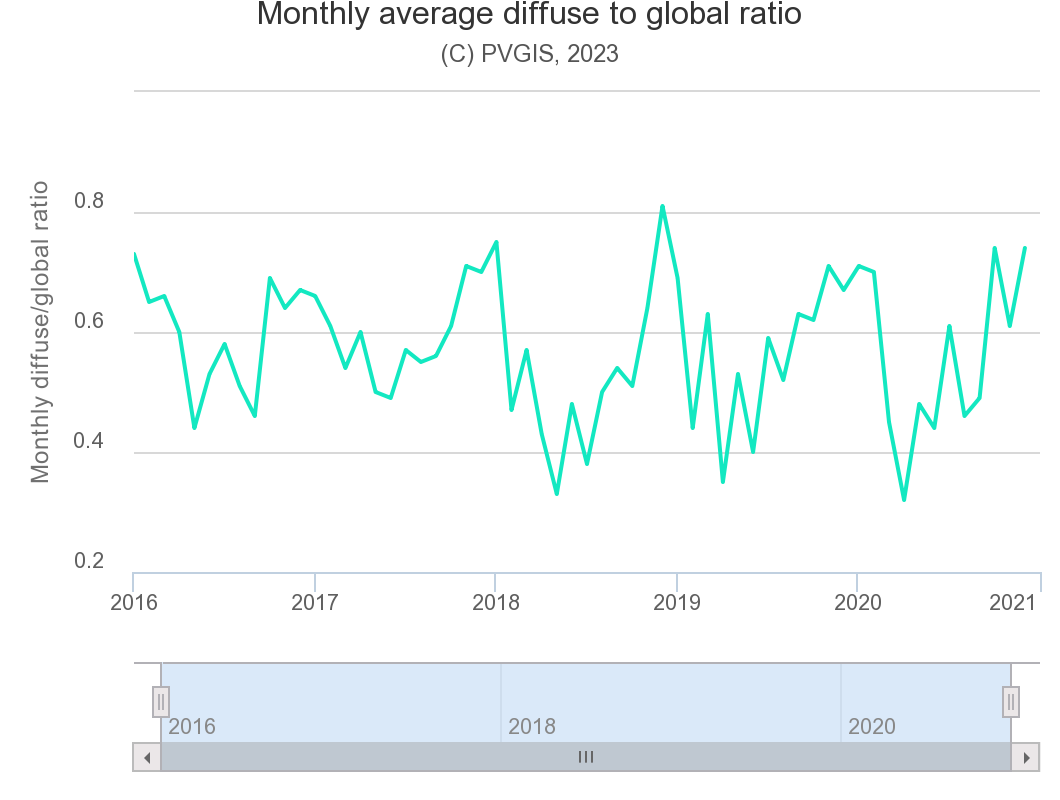 Diffusanteil, monatliche Mittelwerte der Jahre 2016-2020, Hamburg.
Daten generiert mit PVGIS.
Diffusanteil, monatliche Mittelwerte der Jahre 2016-2020, Hamburg.
Daten generiert mit PVGIS.
Beim isotropen Ansatz geht man davon aus, dass die Diffusstrahlung gleichmäßig von jedem Punkt des Himmels kommt. Das ist eine passende Annahme, wenn der Himmel gleichmäßig und stärker bewölkt ist oder bei Nebel. Bei dünnen Wolken kommt die Diffusstrahlung jedoch verstärkt aus der Richtung der Sonne. Nach dem isotropen Ansatz kann die Diffusstrahlung aus dem Diffusanteil und dem Neigungswinkel berechnet werden. Eine horizontale Fläche sieht den ganzen Himmel und nimmt daher die ganze Diffusstrahlung auf. Ein senkrecht stehender Solargenerators sieht nur noch die Hälfte des Himmels und nimmt daher nur die Hälfte der Diffusstrahlung auf.
 Isotroper Ansatz zur Diffusstrahlung auf eine geneigte Ebene. Im Fall eines senkrecht stehenden Solargenerators ist nur noch die Hälfte der Strahlung nutzbar.
Isotroper Ansatz zur Diffusstrahlung auf eine geneigte Ebene. Im Fall eines senkrecht stehenden Solargenerators ist nur noch die Hälfte der Strahlung nutzbar.
Quelle: K. Mertens, www.lehrbuch-photovoltaik.de, Bild 2.17.
Anteil der reflektierten Strahlung
Entgegengesetzt verhält es sich mit dem Anteil der reflektierten Strahlung, Gr / G.
Eine horizontale Fläche sieht nichts vom Boden.
Ein senkrecht stehender Solargenerators sieht nur noch die Hälfte des Bodens (z.B. nach Süden, aber nicht den Boden nach Norden)
und nimmt daher nur die Hälfte der reflektierten Strahlung auf.
Jetzt könnte man vermuten, dass es egal ist für die Summe aus Diffusstrahlung und reflektierter Strahlung,
wie die Fläche ausgerichtet ist. Das ist aber nicht so. Die Diffusstrahlung steigt mit dem Diffusanteil.
Die reflektierte Strahlung reflektiert sowohl Direktstrahlung als auch Diffusstrahlung,
aber nur mit einem verringerten Anteil, dem Reflexionsfaktor (reflection factor), ρ.
Das Verhältnis der reflektierten zur einfallenden Strahlung wird auch
Albedo (albedo) genannt.
Für eine normal "gemischte" Umgebung eines Solargenerators wird ρ = 0,2 gesetzt.
Hohe Werte erreicht nur Schnee: ρ = 0,7.
Gesamte Strahlung auf die geneigte Fläche
Zusammen erhält man die Gleichung für die Strahlung auf eine geneigte Fläche (in Anlehnung an Duffie, 1980, Gl. 2.15.7)
mit
Zur Berechnung der Globalstrahlung an einem wolkenlosen Tag auf eine geneigte Fläche, Gc,t
ist ein Excel-Programm nach Duffie (1980, Ch. 2.8) vorhanden (Download auf Nachfrage). 
|
Beispielrechnung
Möglich ist eine einfache Rechnung dann, wenn die Module nach Süden ausgerichtet sind und die Sonnen ebenfalls im Süden steht. Dann gelten für θ und θz die einfachen Gleichung aus der Aufgabe von oben. Es wird eine Beispielrechnung gemacht, mit den Daten aus dieser Aufgabe. Der Neigungswinkel ist hier aber variabel. Geographischen Breite von ϕ = 50°, 16.05. eines Jahres, Deklination am 16.05. ist δ = 19°. Die Globalstrahlung auf die horizontale Ebene wird angenommen mit 100 W/m2. Von diesem Wert kann gut auf andere Werte der Globalstrahlung umgerechnet werden. Beispiel: GHI = 1000 kWh/m2 (pro Jahr); Tageslicht: 1 Jahr = 365·12 h = 4380 h; daher ist eine durchschnittliche Globalstrahlung eher G = 228 W/m2. Direkt- und Diffusstrahlung werden hier angenommen mit einem Anteil von Gd / G = Gb / G = 0,5 (das ist ein typischer Mittelwert für Deutschland). Für den Reflexionsfaktor (auch: Albedo) wird der typische Wert ρ = 0,2 gewählt.
Interpretation: Die Direktstrahlung erreicht den höchsten Wert, wenn die Sonne senkrecht auf die Module scheint. Das ist bei θ = 0°. Damit gilt für die einfache Rechung (Module nach Süden ausgerichtet; mittags):
Für die Direktstrahlung mittags an diesem Tag ist der optimale Neigungswinkel, βopt = 50° - 19° = 31° (gelbe Kurve im Bild). Für die Diffusstrahlung (isotroper Ansatz) ist der optimale Neigungswinkel immer β = 0°. Die reflektierte Strahlung steigt zwar leicht mit dem Neigungswinkel an, kann aber kaum einen Unterschied machen. Das Optimum der Globalstrahlung der geneigten Fläche ist mittags an diesem Tag βopt = 25° (rote Kurve im Bild). Durch den Diffusanteil wird der optimale Neigungswinkel aus der Direktstrahlung also zu kleineren Winkeln verschoben. |
Dass die Situation i.d.R. komplizierter ist, zeigt das Bild im Abschnitt Geneigte Fläche und Sonnenstand. Der Winkel zwischen der Strahlungsrichtung und der Senkrechten auf der Fläche, der Einfallwinkel, θ wird nach Duffie (1980, Gl. 1.6.2) und nach der Gleichung im Abschnitt Geneigte Fläche und Sonnenstand berechnet. Dieser Winkel, θ im dreidimensionalen Raum hängt ab vom Neigungswinkel, β und von der Höhe der Sonne über dem Horizont – abhängig von Tageszeit und Jahreszeit und damit auch von der Deklination (declination), δ. Weiter hängt θ ab vom Azimut der Fläche, γ und vom Stand der Sonne zur Südrichtung, γs während sie von Ost nach West über den Himmel wandert. γs ist der Stundenwinkel (hour angle) auch bezeichnet mit ω. Wenn θ und dazu noch der Zenitwinkel, θz (Duffie 1980, Gl. 1.6.4) berechnet wurden, dann kann endlich auch das Verhältnis der Direktstrahlung auf die geneigte Fläche, Gb,t zur Direktstrahlung auf die horizontale Fläche, Gb berechnet werden.
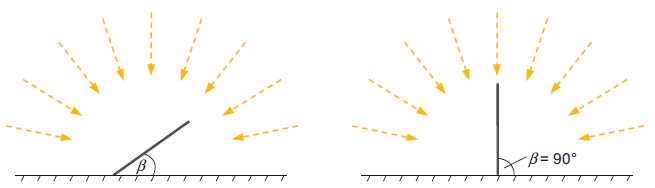
Mehr zum Diffusanteil
Mit dem durchschnittlichen Wetter eines Monats kann der Diffusanteil über die Stunden eines Tages aufgetragen werden.
Der Diffusanteil ist größer bei tiefem Sonnenstand und bei Wolken (Januar).
Dann mag in Deutschland ein Tag in einem bewölkter Wintermonat (Januar) einen Diffusanteil von 0,7 haben und ein Sommermonat (Juli) einen Diffusanteil von 0,5.
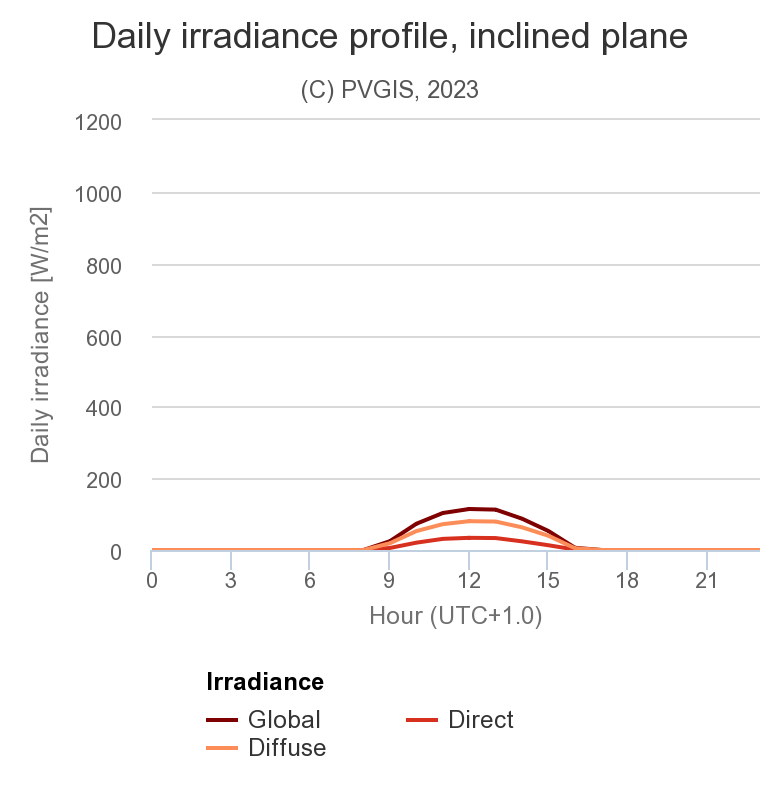
 Durchschnittliche Strahlungsanteile β = 0° im Januar (links) und Juli (rechts), Hamburg.
Daten generiert mit PVGIS.
Durchschnittliche Strahlungsanteile β = 0° im Januar (links) und Juli (rechts), Hamburg.
Daten generiert mit PVGIS.
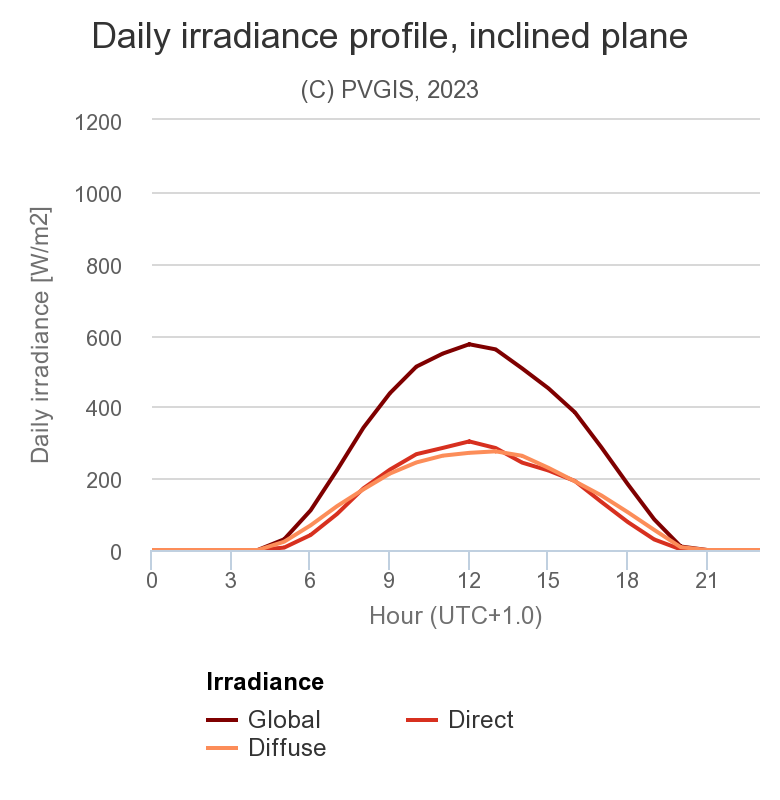
Beim Neigungswinkel β = 37° ist die Globalstrahlung auf der geneigten Fläche durch die reflektierte Strahlung kaum höher als die Summe aus Direktstrahlung und Diffusstrahlung. Die Direktstrahlung nimmt zu durch die bessere Ausrichtung zur Sonne. Damit nimmt der Diffusanteil ab gegenüber der Situation mit horizontaler Fläche.
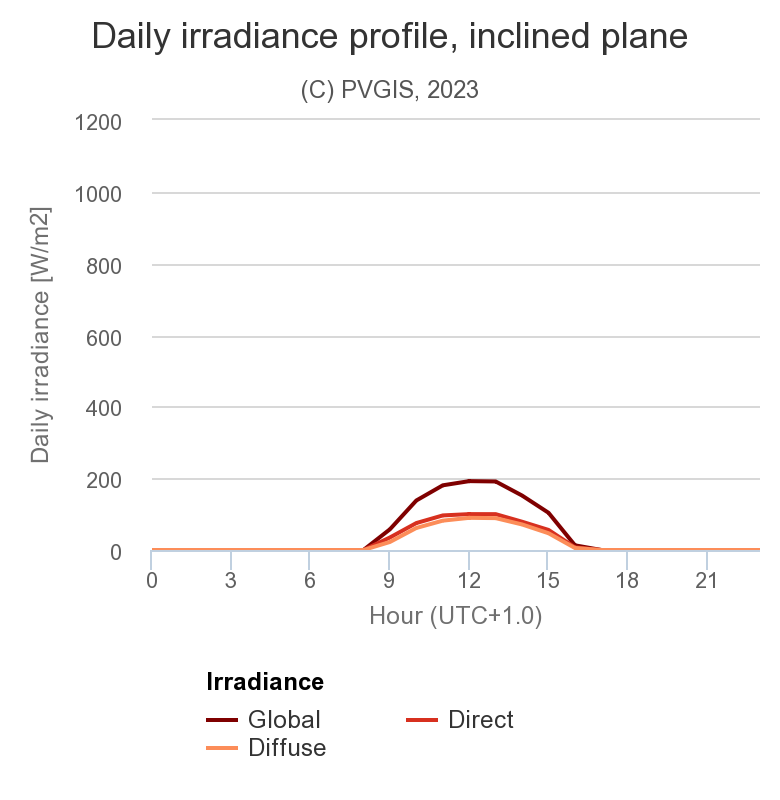
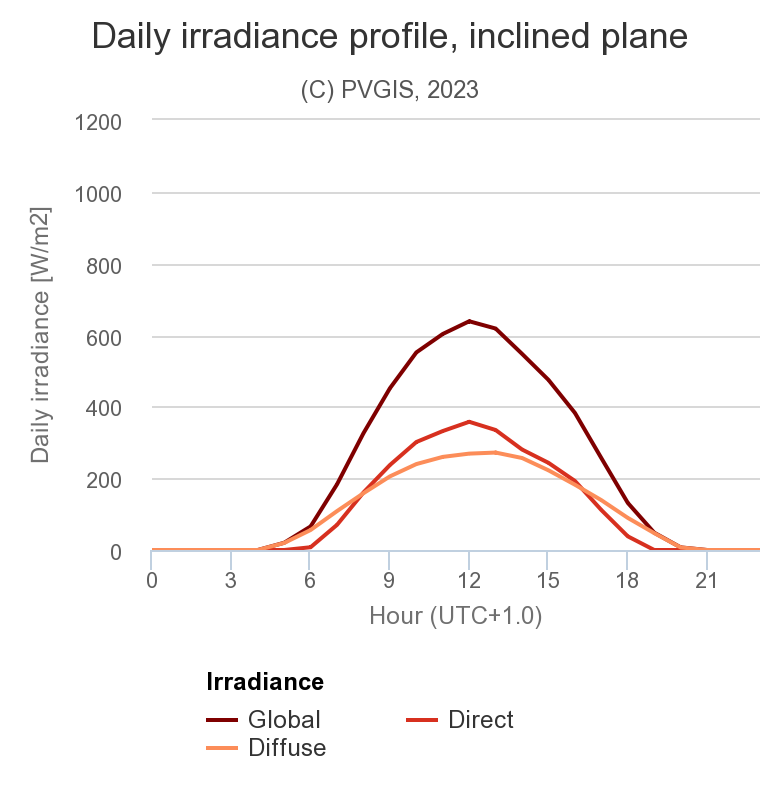 Durchschnittliche Strahlungsanteile β = 37° im Januar (links) und Juli (rechts), Hamburg.
Daten generiert mit PVGIS.
Durchschnittliche Strahlungsanteile β = 37° im Januar (links) und Juli (rechts), Hamburg.
Daten generiert mit PVGIS.
Bei starker Sonneneinstrahlung (Sahara, Juli) ist der Diffusanteil mittags sehr gering (0,2).
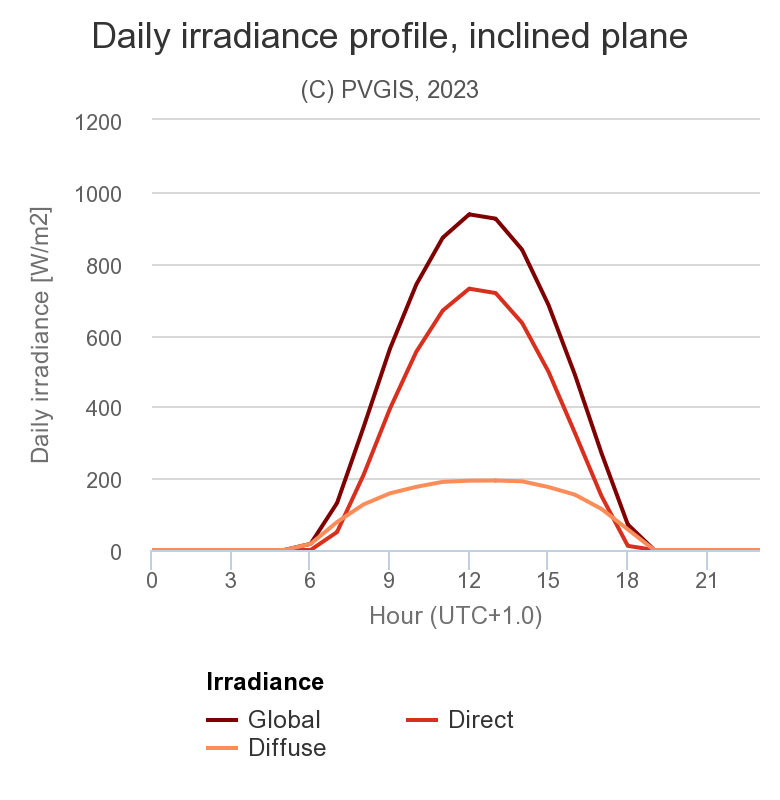 Durchschnittliche Strahlungsanteile β = 30° im Juli, Sahara.
Daten generiert mit PVGIS.
Durchschnittliche Strahlungsanteile β = 30° im Juli, Sahara.
Daten generiert mit PVGIS.
Ein Diffusanteil aus Stundenwerten kann für eine Simulationsrechnung konstant für jede Minute der Stunde herangezogen werden.
Im nächsten Schritt müssen die Klimadaten berücksichtigt werden. Viele Parameter ändern sich ständig: Einfallwinkel (Sonnenlauf), Globalstrahlung auf die geneigte Fläche (wie oben ausgeführt), Wind, Temperatur der Module, ... Aus diesem Grund wird in kleinen Zeitschritten von einer Minute bis zu einer Stunde gerechnet, um so das ganze Jahr abzudecken. Die Globalstrahlung (Leistung pro Fläche) wird über das Jahr addiert. So erhält man die Energie pro Fläche. Diese Art der Berechnung wird in der Praxis mit Solar-Simulationsprogrammen mit der Zeitschritt-Simulation gemacht. Siehe unten: Strahlungssumme mit Klimaeinflüssen und Planungssoftware.
Die Strahlungssumme (irradiation, insolation), H ist die Globalstrahlung, G integriert (aufsummiert) über eine Zeitspanne. Dies ergibt eine Energie pro Fläche, angegeben in kWh/m2 oder in MJ/m2. 1 kWh = 3,6 MJ (Herleitung: 1 kWh = 3600 kWs und 1 Ws = 1 J). Ohne weitere Angaben bezieht sich die Strahlungssumme auf eine horizontale Fläche (β = 0°).
Die Jahressumme (annual irradiation), H (ohne Index) ist die Energie pro Fläche aufsummiert über ein Jahr und hat die Einheit kWh/m2 (pro Jahr). Gelegentlich wird auch angegeben die Monatssumme (monthly) Hm aufsummiert über einen Monat mit der Einheit kWh/m2 (pro Monat) oder die Tagessumme (daily) Hd aufsummiert über einen Tag mit der Einheit kWh/m2 (pro Tag).
Wie bei der Globalstrahlung wird auch bei der Strahlungssumme weiter differenziert und unterschieden hinsichtlich der Art der Strahlung und der Ausrichtung der Fläche:
Eine klassische Handbuchmethode wie man die Monatssummen, Hm ermitteln kann, wird von Duffie (1980) in Abschnitt 2.7 vorgestellt. Die Ausgangsgleichung ist
Diese historische Methode liefert praxisgerechte Strahlungswerte. Für einen Klimatyp sind die Parameter a und b gegeben. Für den eigenen Standort benötigt man zusätzlich die relative Sonnenscheindauer. Falls nicht gegeben könnte ein Sonnenscheinautograph genutzt werden. Dessen Betrieb und Auswertung erfordert viel Zeit. So ist man aber früher vorgegangen. Die Methode wird weiter unten vorgestellt.
Statt der alten Handbuchmethoden bezieht man heute die Strahlungsdaten aus dem Internet. Dazu gibt es zwei gute Quellen:
Dies wird erklärt im Abschnitt Rechnen mit Wirkungsgraden.
Strahlungssummen aus dem Global Solar Atlas (GSA)
Die Startseite des Global Solar Atlas (GSA) ist
https://globalsolaratlas.info/map  .
Oben links bei "Search location" wird der Ort oder der Staat eingegeben, für den die Strahlungswerte gesucht werden.
.
Oben links bei "Search location" wird der Ort oder der Staat eingegeben, für den die Strahlungswerte gesucht werden.
Verschiedene Kartendarstellungen sind verfügbar:
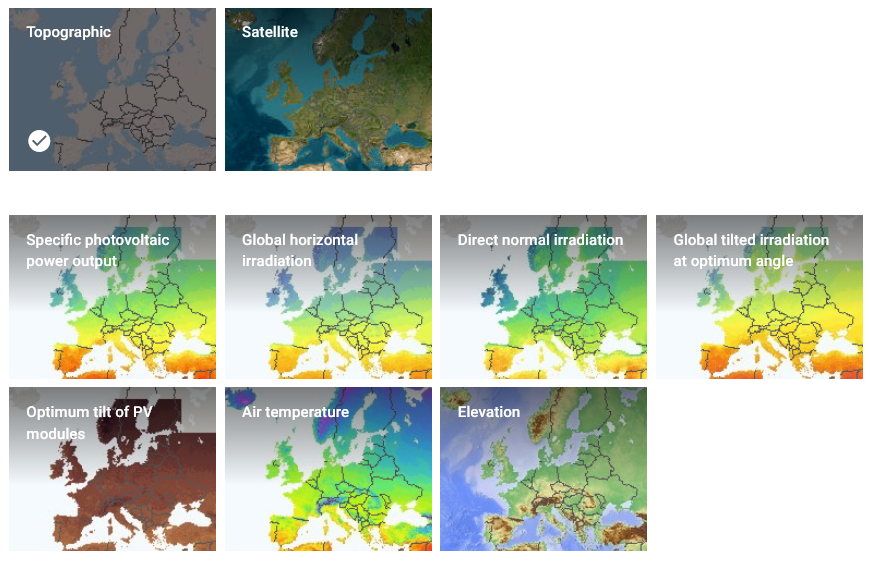
|
Topographic Satellite PVOUT (specific photovoltaic power output), dies ist E*AC GHI (global horizontal irradiation) DNI (direct normal irradiation) GTI_opta (global tilted irradiation at optimum angle) OPTA (optimum tilt of PV modules) TEMP (air temperature) ELE (elevation) |
GSA bietet Karten mit PVOUT, GHI und DNI für einzelne Staaten zum Download. Das Ablesen aus der Karte ist etwas weniger genau als die numerischen Daten für jeweils einen Ort.
Für Norddeutschland kann aus der Karte abgelesen werden H = 950 kWh/m2.
Daten aus dem Global Solar Atlas für Hamburg zeigen (in grün) eine Strahlungssumme auf eine horizontale Fläche, H von sogar 1016 kWh/m2, wir merken uns H = 1000 kWh/m2.
Daten aus dem Global Solar Atlas für Hamburg zeigen (in grün) eine Strahlungssumme auf eine optimal geneigte Fläche, Ht,opt von 1200 kWh/m2. Der Wert ist (wegen der besseren Ausrichtung) etwas höher als der Wert für die horizontale Fläche.
Der spezifische Ertrag, E*AC wird angegeben mit 975 kWh/kWp. In der Angabe ist (unausgesprochen) ein Anlagenwirkungsgrad (performance ratio) enthalten von PR = 975/1200 = 81,25 %. Das ist ein realistischer Wert. Weiterhin realistisch wäre ein Wert von PR = 1000/1200 = 83,33 %.
Wir merken uns, dass in Hamburg mit einem Anlagenwirkungsgrad, PR = 83 % ein spezifischer Ertrag, E*AC erreicht wird von 1000 kWh/kWp.
Strahlungssummen aus dem Photovoltaic Geographical Information System (PVGIS)
Das
Photovoltaic Geographical Information System (PVGIS)
liefert verschiedenen Daten. TMY steht für "Typisches Meteorologisches Jahr" ("Typical Meteorological Year").
Das TMY liefert die Eingangsdaten für eine eigene PV-Berechnung.

Die erste Berechnung liefert die
Leistung einer Anlage mit Volleinspeisung in das Netz  ("NETZGEKOPPELT" bzw. "GRID CONNECTED")
für einen gewählten Ort. Die
Dokumentation
erklärt die Benutzung des Tools.
PVGIS liefert weiterhin
auf einer Karte
die Strahlungssummen für Deutschland und für andere Länder zum optimalen Winkel der Module und auf die Horizontale.
("NETZGEKOPPELT" bzw. "GRID CONNECTED")
für einen gewählten Ort. Die
Dokumentation
erklärt die Benutzung des Tools.
PVGIS liefert weiterhin
auf einer Karte
die Strahlungssummen für Deutschland und für andere Länder zum optimalen Winkel der Module und auf die Horizontale.
Aus der Legende wird deutlich, dass die Strahlungssumme multipliziert mit dem Anlagenwirkungsgrad (performance ratio), PR den Ertrag ergibt. Im Beispiel ist die Skala so beschriftet, wie es sich für PR = 75 % ergibt. Es ist z.B. 1200 · 0,75 = 900.
Eine Umrechnung der Strahlungssumme, H zur horizontalen Fläche auf die Strahlungssumme, Ht zur geneigten Fläche ist in der Regeln nicht erforderlich, weil man die Daten für die geneigte Fläche bereits aus dem Internet mit Hilfe von GSA oder PVGIS bezieht (siehe oben). Trotzdem ist es hilfreich diese Umrechnung zu kennen. Diese Umrechnung ...
Hat man beispielsweise die Module mit 20° Neigungswinkel nach Osten ausgerichtet, dann wäre am Beispiel Hamburg (siehe Bild) Ht = H · 83,8/87,1.
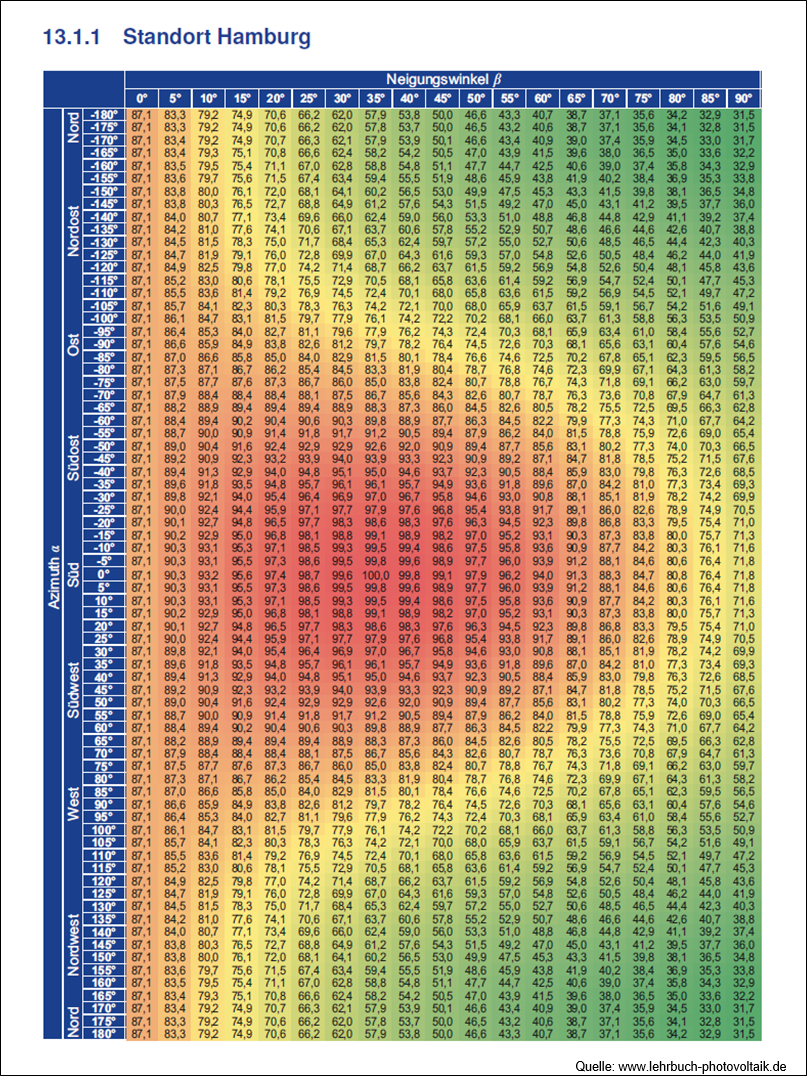
Werden die Module nicht optimal ausgerichtet, dann tritt eine Minderleistung ein.
Die Zahlen im Diagramm kann man als einen Wirkungsgrad der Modulausrichtung, ηβ,λ (in Prozent) auffassen.
Quelle: K. Mertens, www.lehrbuch-photovoltaik.de
In diesem Abschnitt werden zunächst die Standardtestbedingungen für PV-Module angegeben und die Nennleistung einer PV-Anlage definiert. Strahlungsparameter und Erträge werden auf die Nennleistung bezogen. Das liefert spezifische Erträge und Volllaststunden.
Standardtestbedingungen, GSTC und Nennleistung, PSTC
In der Photovoltaik sind
Standardtestbedingungen
(Standard Test Conditions, STC) definiert:
Spezifischer Ertrag
Spezifischer Ertrag bedeutet Ertrag pro Nennleistung.
Der Ertrag ist die Energie, die während einer bestimmten Zeit (i.d.R. ein Jahr) unter gegebenen realen Strahlungsbedingungen
bereitgestellt werden kann bezogen auf eine definierte Nennleistung (unter Standardbedingungen).
Die Standardbedingungen sind in der Photovoltaik definiert. Siehe oben.
Strahlungssummen, H auf die horizontale Fläche, oder auf eine geneigte Fläche (tilt) werden auf eine Einstrahlung unter Standard-Testbedingungen (STC), GSTC bezogen. Ausgangsenergien werden auf die Nennleistung der Anlage, PSTC in kWp bezogen. Ich benutze einen hochgestellten Stern (*), um anzuzeigen, dass es sich um eine spezifische Größe handelt bezogen auf Nennleistung. Das hat den Vorteil, dass der Zusammenhang zwischen der ursprünglichen Größe und der spezifischen Größe sichtbar bleibt. Der spezifische Ertrag (yield) wird im englischsprachigen Raum mit Y bezeichnet. Definiert ist: der spezifische Ertrag (yield) der Strahlungssumme auf die geneigte Fläche als Referenz am Eingang (Reference), YR, die Energie (Gleichstrom, Direct Current, DC) am Ausgang des Moduls (Array), YA und die Energie (Wechselstrom, Alternating Current, AC) am Zähler, also bei der Übergabe in das Netz (Final), YF. Verschiedene spezifische Erträge können so definiert werden.
Volllaststunden
Wer möchte kann zum weiteren Verständnis erfahren, dass der spezifischer Ertrag identisch ist mit den Volllaststunden.
Das hat in der Praxis lediglich den Vorteil, dass man eine Angabe über "Volllaststunden" (z.B. im Ergebnis einer PV-Simulationsrechnung) als "spezifischer Ertrag" deuten kann.
Es muss dann "nur" noch sichergestellt werden, um welche Volllaststunden es sich handelt, weil hier oben ja bereits vier spezifische Erträge definiert wurden.
Leistung ist Energie pro Zeit, P = E / t. Energie ist Leistung mal Zeit, E = P · t. Also ist Energie pro Leistung, E / P = t, also Zeit. Am Beispiel dieser Einheiten: kWh / kW = h (Stunden).
Viel Zeit wird die PV-Anlage ungünstige Strahlungsbedingungen (Nacht, Wolken) vorfinden. Die Frage ist: Welche Zeit, tFL – wie viele Volllaststunden (full load hours) – müsste die Sonne mit Volllast, GSTC = 1000 W/m2 scheinen, um die gleiche Energie, H zu liefern, wie unter realen Bedingungen?
In Norddeutschland bringt es die Sonne auf tFL = 1000 kWh/m2 / 1 kW/m2 = 1000 h. Dabei betrachten wir die Globalstrahlung auf die horizontale Fläche in Norddeutschland.
In Norddeutschland bringt es die Sonne auf tFL = 1200 kWh/m2 / 1 kW/m2 = 1200 h. Dabei betrachten wir die Globalstrahlung auf die geneigte Fläche in Norddeutschland.
In Norddeutschland bringt es eine PV-Anlage auf tFL = 1000 kWh / 1 kWp = 1000 h. Dabei gehen wir hier aus von der Energie (Wechselstrom, alternating current, AC) am Zähler, also bei der Übergabe in das Netz.
Das Jahr hat 365·24 h = 8760 h. Die (z.B.) 1000 h ergeben somit einen Jahresnutzungsgrad (capacity factor) von 11,4 % bezogen auf die Stunden im Jahr. Der Wert ist sehr niedrig. Das liegt daran, dass man durch die Stunden des ganzen Tages teilt – also auch durch die Stunden der Nacht. Der Jahresnutzungsgrad darf also nicht mit einem Wirkungsgrad verwechselt werden. Es lassen sich viele Beziehungen aufstellen. Nicht alles erhöht das Verständnis. Nicht alles muss man machen.
Von der Solarkonstante Gsc bis zur Einspeisung der Leistung als Wechselstrom (alternating current, AC) in das Netz mit PAC geht an vielen Stellen Leistung verloren. Der Wirkungsgrad, η ist jeweils die Ausgangsleistung geteilt durch die Eingangsleistung. An jeder Komponente, i dokumentiert der Wirkungsgrad ηi = PA,i / PE,i den Verlust. ηi < 1. Statt des Wirkungsgrades wird oft auch ein Verlust (loss), L in Prozent (%) für eine Komponente oder einen Sachverhalt angegeben. Der Verlust kann in einen Wirkungsgrad umgerechnet werden. Ein Verlust von 2 % = 0,02 durch eine Komponente ergibt einen Wirkungsgrad dieser Komponente von 0,98. Auf diese Weise können wahlweise Verluste oder Wirkungsgrade benannt werden. Die Rechnung sollte aber einheitlich mit Wirkungsgraden durchgeführt werden.
Wirkungsgrade werden durch Multiplikation zusammengefasst.
Wenn es fünf Komponenten gibt mit je 5 % Verlust, dann hat jede Komponente einen Wirkungsgrad von 0,95. Multipliziert ergibt das einen Wirkungsgrad, η von 0,955 = 0,774. Man darf also nicht den Fehler machen, die Verluste zu addieren (25 %) und danach erst den Wirkungsgrad zu berechnen: 0,75 (falsch!). Daher:
Wirkungsgradkette – Prinzipdarstellung
Die Ausgangsleistung der ersten Komponente ist die Eingangsleistung der zweiten Komponente, ... u.s.w.
Daher sind die Wirkungsgrade in einer langen Kette angeordnet.
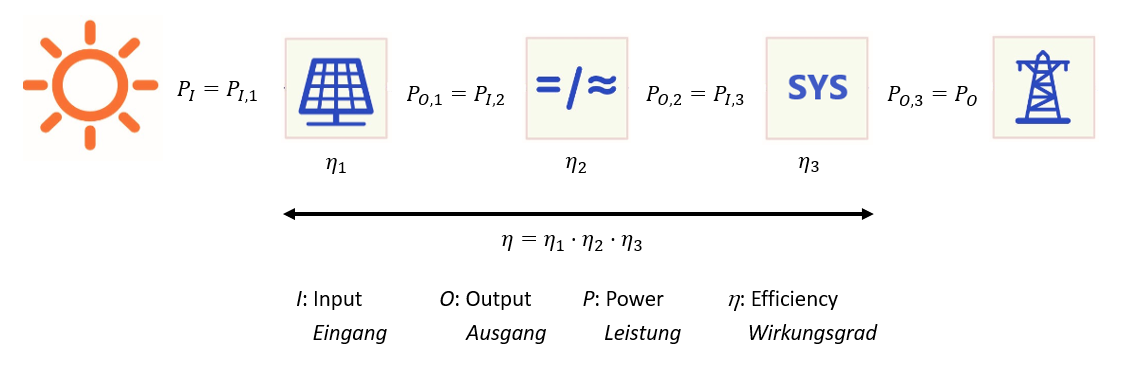
Prinzipdarstellung(!) der Wirkungsgrade, η einer PV-Anlage in einer langen Kette.
Von der Eingangsleistung der Sonne, über das Solarmodul(1), zum Wechselrichter(2) und die "sonstigen Komponenten und Verluste im System (SYS)"(3) zum Ausgang und
damit zur Einspeisung in das Netz.
Wirkungsgradkette – Photovoltaik
Von der Prinzipdarstellung geht es zu den Parametern, wie sie für diese Darstellung mit Bedacht und normgerecht ausgewählt wurden.
Es ist eine Darstellung basierend auf dem Sprachgebrauch und dem Vorgehen aus der Praxis, aber mit einer eigenen Didaktik.
Anhand der Symbole wird unterschieden: die Sonne, das Solarmodul (solar module, MOD),
Wechselrichter (inverter, INV), "sonstige Komponenten und Verluste im System" (SYS) und das Stromnetz.
Es ist nur die Volleinspeisung in das Netz gezeigt. Eine erweiterte Darstellung mit Eigenverbrauch und/oder Batterien könnte sich anschließen.
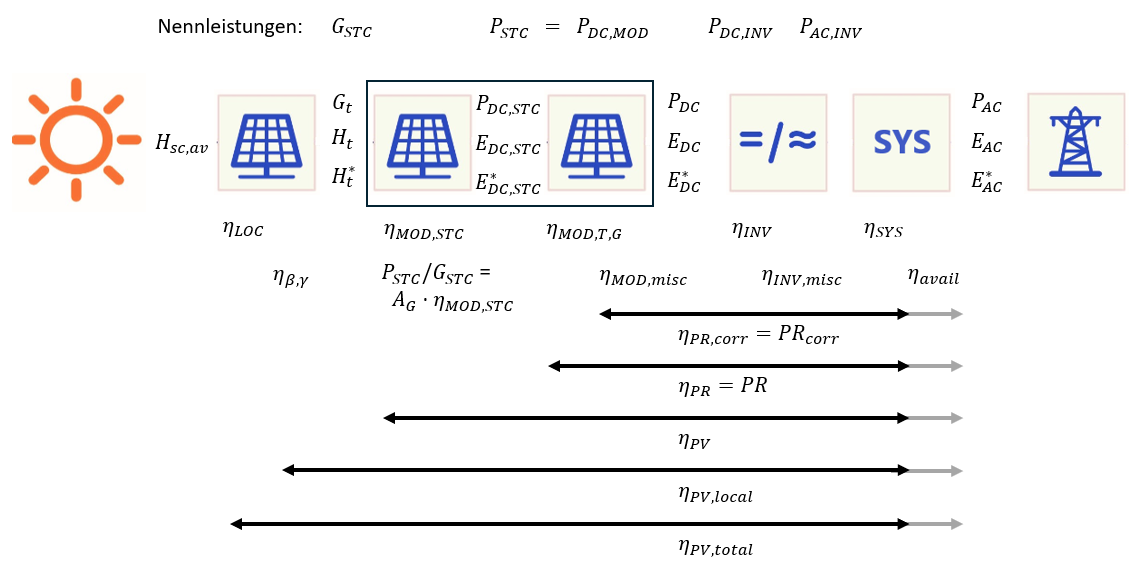
Die Wirkungsgrade, η einer PV-Anlage in einer langen Kette.
Nur die Volleinspeisung in das Netz ist gezeigt.
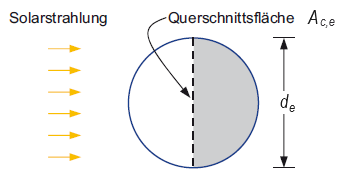
Querschnittsfläche und Kugeloberfläche zur Bestimmung der durchschnittlichen Globalstrahlung auf die Erdoberfläche.
Nach: K. Mertens, www.lehrbuch-photovoltaik.de, Bild 2.21.
Ein Blick in eine Formelsammlung liefert die Formel für die Kreisfläche als Funktion vom Radius, r = d/2 und die Formel für die Kugeloberfläche. Beides angegeben für den Radius der Erde, re ist
.
Die sich auf die Kugeloberfläche verteilende durchschnittliche Solarstrahlung (Tag- und Nachtseite) beträgt also
.
Multipliziert mit 24 Stunden und 365 Tagen ergibt dies über die Erde (und über Tag und Nacht) verteilt durchschnittlich (average)
.
An keinem Ort der Erde kommt so viel Energie am Erdboden (horizontal) an, wie es der durchschnittlichen extraterrestrischen Strahlungssumme, Hsc,av entspricht. Dies, weil die Sonne an keinem Ort der Erde den ganzen Tag senkrecht steht. Dies weiterhin aufgrund der Verluste beim Durchgang der Strahlung durch die Atmosphäre. Dies, obwohl die Strahlung auf die Tag und Nachtseite der Erdoberfläche verteilt wurde.
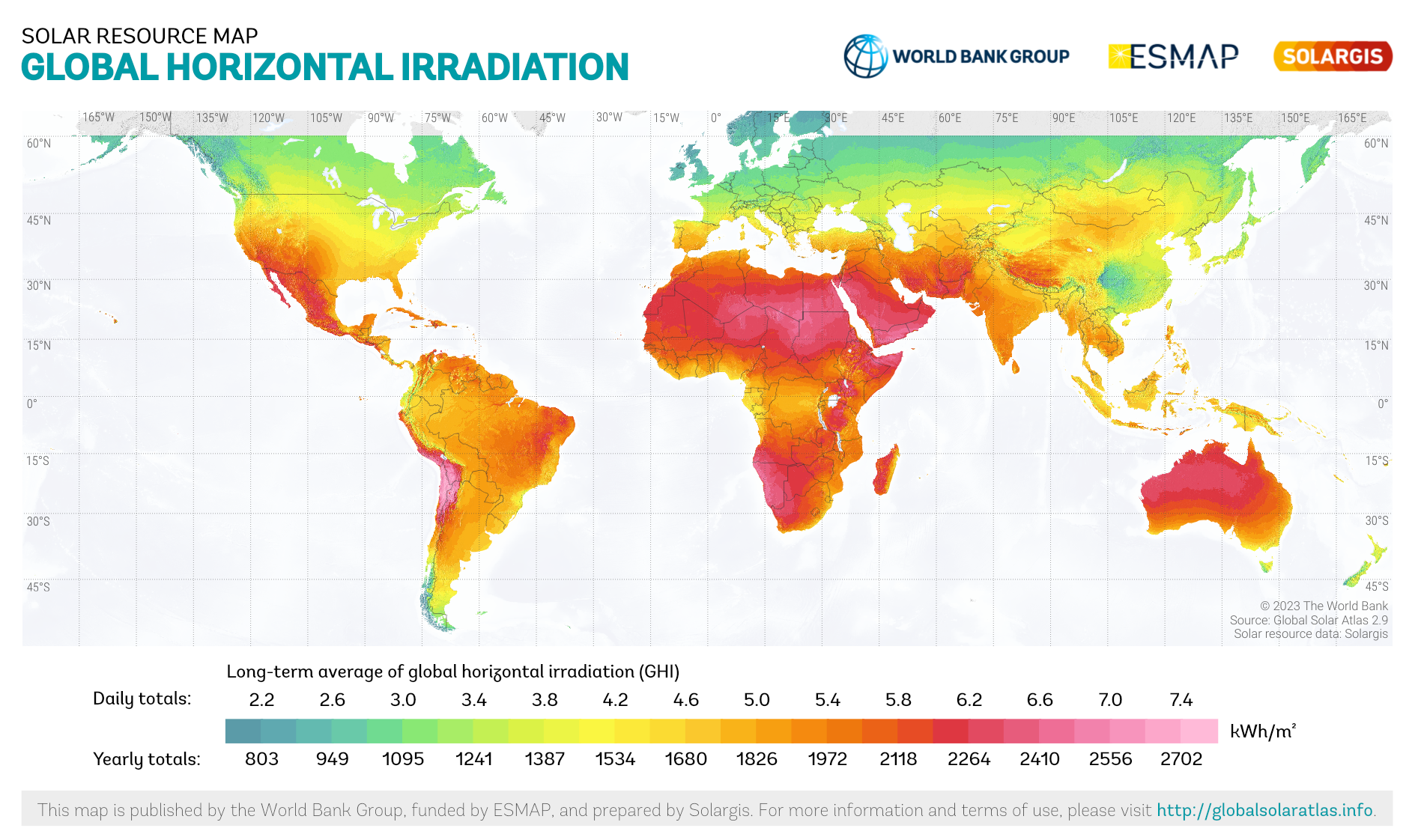
Strahlungssummen auf die horizontale Fläche an verschiedenen Stellen der Erde.
Standard-Wirkungsgrad zum geographischen Ort, ηLOC (efficiency of geographical location)
Dieser Wirkungsgrad wird definiert mit H = GHI.
Trotz der uneinheitlichen Verteilung der Globalstrahlung gibt es einen generellen Trend: An Orten großer geographischer Breite, ϕ kommt wenig Strahlung an. In Richtung der Pole steht die Sonne nie hoch am Himmel. Eine Solaranlage sollte daher nicht zu weit im Norden (genauer: in Richtung der Pole) aufgebaut werden.
Fazit: Es gibt nur wenige (dichter besiedelte) Gebiete auf der Erde, die für PV noch weniger geeignet sind als Deutschland. Bei den Gebiete, die weniger geeignet sind als Deutschland handelt es sich um Irland, Schottland, Skandinavien und Kanadas Westküste. Andere Gebiete erhalten bis zum dreifachen der Solarstrahlung. Trotzdem: PV geht auch in Deutschland. Außerdem muss die Erzeugung in der Nähe des Verbrauchs stattfinden. Da bleibt keine Wahl.
Alternativ-Wirkungsgrad zum geographischen Ort, ηLOC,opt (alternative efficiency of geographical location)
Dieser Wirkungsgrad wird definiert mit Ht,opt = GTI, also mit der Strahlungssummen auf die optimal geneigte Fläche.
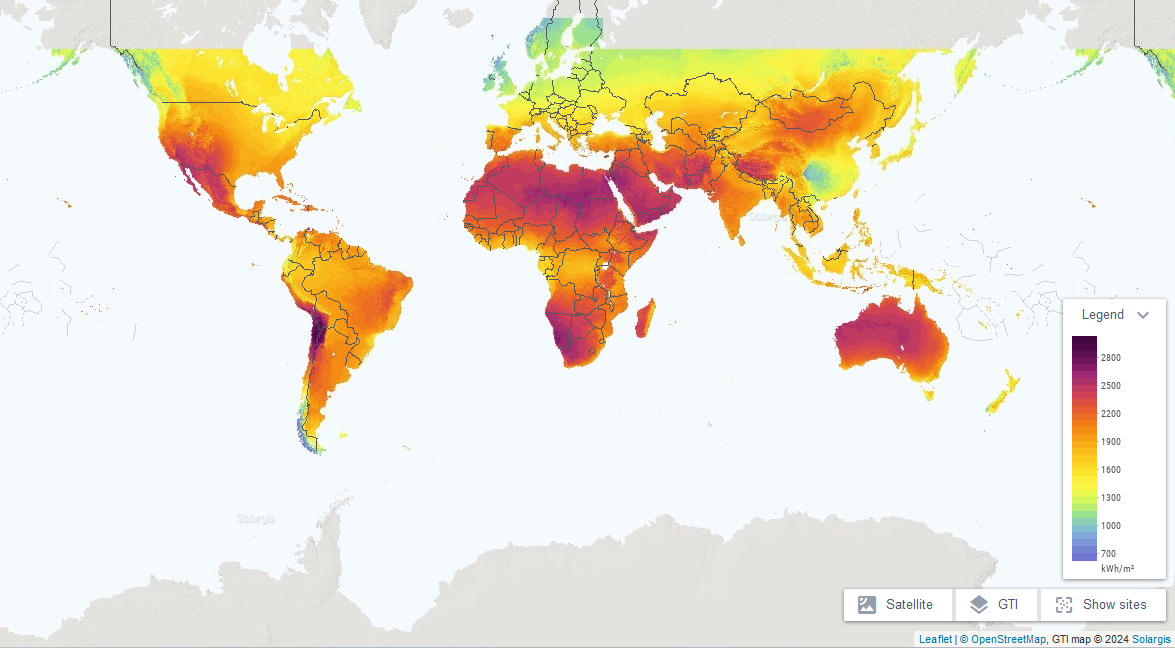
Strahlungssummen auf die optimal geneigte Fläche an verschiedenen Stellen der Erde.
In einer Gegend der Erde kommen (zufällig und ziemlich genau) 100 % der als Hsc,av definierten Strahlungssumme auf einer optimal geneigten Fläche an. Dies ist der Fall an verschieden Orten auf der Ostflanke der Cordillera Domeyko, die den westlichen Abschluss des Nationalpark Llullaillaco in den Anden von Chile bilden. Hier einer dieser Punkte, die die höchsten Strahlungssummen weltweit auf einer optimal geneigten Fläche mit recht genau 2981 kWh/m2 aufweisen. Der optimale Neigungswinkel beträgt hier 26°. ηLOC,opt = 100 %. Allgemein gilt
.
Der Vorteil dieser Darstellung mit ηLOC,opt und Ht,opt ist, dass im nächsten Schritt beim Wirkungsgrad ηβ,λ keine Werte größer als 1 auftreten und dass der Wirkungsgrad ηβ,λ direkt aus dem Anlagenkennfeld abgelesen werden kann, ohne eine Umrechnung. Der Nachteil dieser Beschreibung ist, dass die Strahlungssummen auf die optimal geneigte Fläche bekannt sein müssen. Diese sind weniger verbreitet. Weiterhin muss gleichzeitig auch der optimale Neigungswinkel bekannt sein. Der optimale Neigungswinkel hängt von Details des Klimas vor Ort ab. Hier der optimale Neigungswinkel an verschiedenen Stellen der Erde.
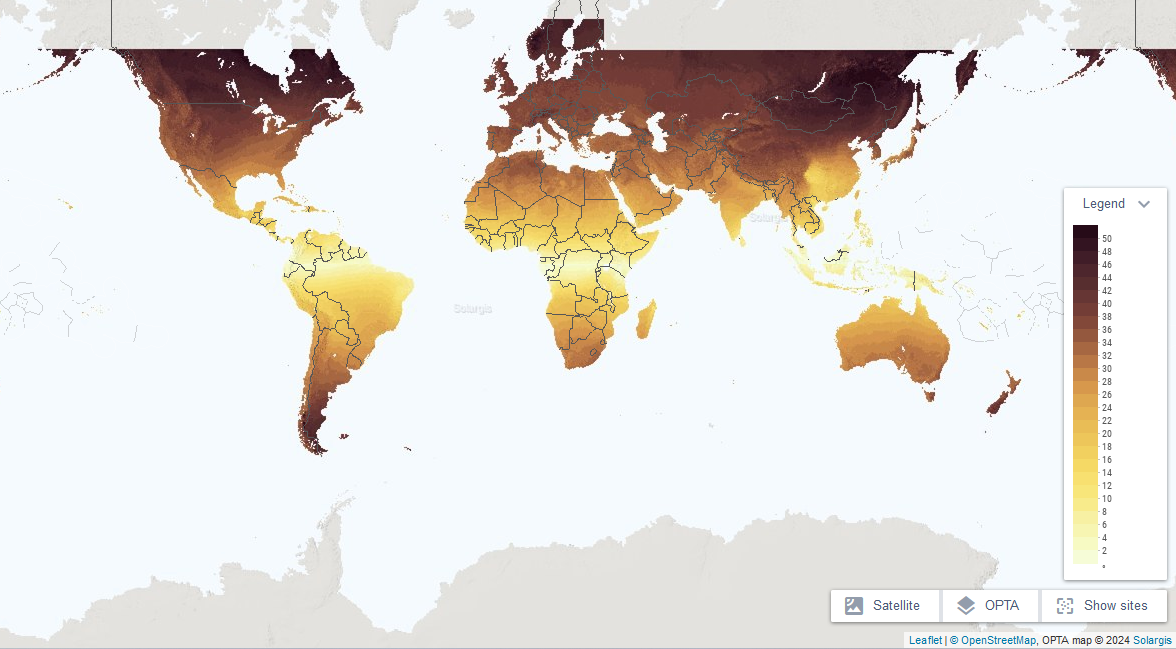
Karte mit dem optimalen Neigungs für die verschiedenen Orte der Erde.

Auf der Ostflanke der Cordillera Domeyko treten die höchsten Strahlungssummen der Erde auf –
sowohl auf die horizontale Fläche, wie auch auf die optimal geneigte Fläche.
Die Cordillera Domeyko bilden den westlichen Abschluss des Nationalpark Llullaillaco (gezeigt hier im Bild).
Die Cordillera Domeyko sind ein Gebirgszug in den Anden im Norden von Chile. Quelle: "Chile365", CC BY-SA, Wikipedia.
Die Anlage sollte mit optimalem Neigungswinkel, β und Azimut, γ aufgebaut werden. Das wird durch den Wirkungsgrad der Modulausrichtung, ηβ,λ ausgedrückt. Werte für den Wirkungsgrad können dem Anlagenkennfeld für Hamburg oder oben auch für Berlin oder München entnommen werden. Der so definierte "Wirkungsgrad"
kann ausnahmsweise Werte größer als eins annehmen – am Beispiel Hamburg bis zu einem Wert ηβ,λ = 1/0,871 = 1,148. Das liegt daran, dass in dieser Darstellung die Solarstrahlung zunächst auf die horizontalen Ebene verteilt wurde, jetzt aber das Modul doch optimaler zur Sonne ausgerichtet wird. Eine alternative Definition der Wirkungsgrade als ηβ,λ,opt mit ηLOC,opt hat diesen Nachteil nicht. Siehe dazu etwas weiter unten.
Oft wird direkt vor Ort in die Betrachtung eingestiegen mit den Werten der Einstrahlung auf die geneigte Fläche mit schon bekannten Winkeln:
Alternativ-Wirkungsgrad zur Ausrichtung der Module, ηβ,λ,opt (alternative efficiency of module orientation)
Dieser Wirkungsgrad wird definiert zusammen mit ηLOC,opt, ausgehend von Ht,opt.
Der Vorteil dieser Darstellung mit ηβ,λ,opt und Ht,opt ist, dass keine Werte größer als 1 auftreten und dass der Wirkungsgrad ηβ,λ direkt aus dem Anlagenkennfeld abgelesen werden kann, ohne eine Umrechnung. Der Nachteil dieser Beschreibung ist, dass die Strahlungssummen auf die optimal geneigte Fläche bekannt sein müssen. Diese sind weniger verbreitet. Weiterhin muss gleichzeitig auch der optimale Neigungswinkel bekannt sein. Der optimale Neigungswinkel hängt von Details des Klimas vor Ort ab.
In der Wirkungsgradkette können wahlweise a) die Standard-Wirkungsgrade bezogen auf die horizontale Fläche oder b) die Alternativ-Wirkungsgrade bezogen auf die optimal geneigte Fläche benutzt werden. Der Wirkungsgrad ηLOC ist kleiner als als ηLOC,opt. Dafür ist der Wirkungsgrad ηβ,λ größer als ηβ,λ,opt.
Beispiel Hamburg (bei optimaler Neigung der Solarmodule):
a) ηLOC · ηβ,λ = 1015/2981·1/0,871 = 0,39
b) ηLOC,opt · ηβ,λ,opt = 1200/2981·1 = 0,40.
Die vergleichsweise kleine Abweichung entsteht, weil Daten aus unterschiedlichen Quellen genutzt werden: a) GSA mit Mertens versus b) nur GSA.
Modulwirkungsgrad bei Standardtestbedingungen, ηMOD,STC
Der Wirkungsgrad eines PV-Moduls ist die Ausgangsleistung / Eingangsleistung.
Die Ausgangsleistung in Form von Gleichstrom (direct current, DC) ist die Nennleistung des Moduls, PDC,MOD = PSTC. Sie wird auf die Brutto-Kollektorfläche (gross collector area) des Moduls, AG bezogen. Das ist die größte projizierte Fläche eines vollständigen Kollektors, ohne Vorrichtungen für die Befestigung. Wir erhalten eine Leistungsdichte in W/m2.
Die Brutto-Kollektorfläche des Moduls ergibt sich aus der im Datenblatt angegebenen Länge mal der Breite.
Die Eingangsleistung ist die Globalstrahlung unter Standardtestbedingungen, GSTC, ebenfalls in W/m2. Der Modulwirkungsgrad bei Standardtestbedingungen ist dann
| Beispiel: Ein Modul hat eine Nennleistung von 0,43 kWp. Die Größe ist 1,722 m x 1,134 m = 1,953 m2. Der Wirkungsgrad beträgt 0,43 / 1 / 1,953 = 22 %. |
Wir schreiben die Größen Leistung, P und Energie, E mit zwei Strichen, wenn sie auf die Modulfläche bezogenen sind. Also: P" und E". Die Größen G und H sind von sich aus bereits auf die Fläche bezogen. Daher dann auch
.
In der Praxis wird man den Wirkungsgrad unter Standardtestbedingungen des Moduls direkt aus dem Datenblatt ablesen!
|
An dieser Stelle soll eine wichtige Umrechnung eingeführt werden.
Es ist der Ausdruck (AG · ηMOD,STC) .
Der Zahlenwert von AG · ηMOD,STC (in m2) ist der gleiche Zahlenwert, wie der der Nennleistung der PV-Anlage (in kWp). |
Die folgenden Parameter: Globalstrahlung der geneigten Fläche, Gt und Strahlungssumme der geneigten Fläche, Ht werden mit dem Produkt (ηMOD,STC · AG) umgerechnet auf idealisierte Werte unter Standard Test Conditions (STC): PDC,STC und EDC,STC. Die spezifische Energie der Strahlungssumme der geneigten Fläche, H*t ist bereits auf GSTC bezogen und daher gleich E*DC,STC .
Diese idealisierten Werte sind nur virtuell. Sie können an keiner Stelle gemessen werden, weil noch andere Verluste hinzukommen, bis sich die Gleichstromausgangsgrößen am Solarmodul ergeben.
Der Modulwirkungsgrad bei Standardtestbedingungen, ηMOD,STC ist mit rund 20 % im Vergleich zu anderen Kraftwerken sehr gering. Das ist einer der Gründe, warum der Wirkungsgrad separat gehalten wird. Ein Wert wie z.B. 20 % entspricht nicht der üblichen Größe eines Wirkungsgrades und macht sich nicht gut im Verkaufsgespräch. Im Unterschied zu anderen Kraftwerken erhält die PV-Anlage den Treibstoff aber von der Sonne kostenlos. Der geringe Modulwirkungsgrad ist daher zu akzeptieren. Am Ende ist es immer eine Frage der Wirtschaftlichkeit.
Temperatur- und Globalstrahlungswirkungsgrad, ηMOD,T,G
Idealerweise liegt ein Wirkungsgradkennfeld für ein Solarmodul vor. Der Temperatur- und Leistungswirkungsgrad ist abhängig von der Leistung der Einstrahlung und von der Temperatur des Moduls. Der Wirkungsgrad sinkt mit steigender Temperatur und mit sinkender Einstrahlung. In einem Moduldatenblatt sind dafür Koeffizienten angegeben. Wo im Kennfeld diese Koeffizienten abzulesen wären ist in rot eingezeichnet.
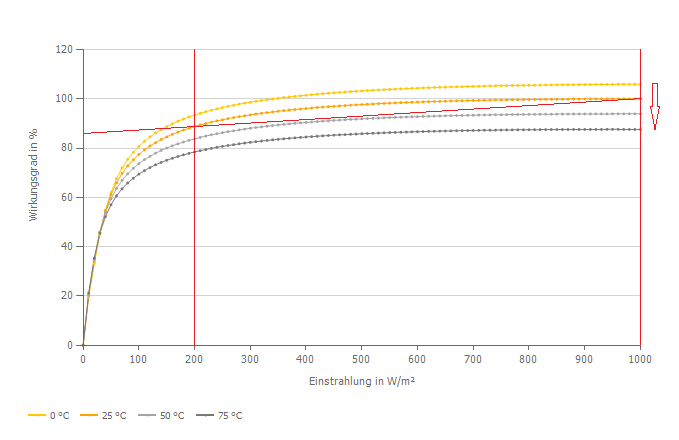
Typischer Verlauf des Modulwirkungsgrads bei unterschiedlichen Modultemperaturen und unterschiedlicher Einstrahlung.
Im Diagramm, am rechten Rand, kann der Temperaturkoeffizienten bei GSTC = 1000 m2 abgelesen werden.
Dieses Kennfeld zeigt einen Temperaturkoeffizienten von -0,26 %/°C.
An der roten diagonalen Linie kann die Abnahme des Wirkungsgrades im Bereich von 1000 W/m2 bis 200 W/m2 bei 25 °C abgelesen werden: 10.0 %.
Quelle: Valentin, 2023: PV*SOL Hilfe > Berechnungsgrundlagen > PV-Module > Modultemperatur. https://help.valentin-software.com
Der Temperatur- und Globalstrahlungswirkungsgrad, ηMOD,T,G kann nur berechnet werden, wenn die Temperatur bekannt ist. Die Temperatur kann im Betrieb gemessen werden. Im Planungsstadium muss die Temperatur berechnet werden. Hier (Archiv) wird gezeigt, wie die Temperatur des Moduls statisch (einfach) oder dynamisch (aufwändiger) berechnet werden kann.
Das Bild oben zeigt, was die Angaben aus dem Datenblatt im Diagramm bedeuten und welche Vereinfachung im Vergleich zum realen Verlauf des Wirkungsgrades das bedeutet. Der Temperaturkoeffizient ist linear (gleiche Abstände zwischen den Kurven) – das passt. Die lineare Approximation der Abnahme des Wirkungsgrades passt weniger gut – insbesondere bei geringer Einstrahlung mit weniger als 200 W/m2. Hier die Werte aus einen Moduldatenblatt.
Werte aus einen Moduldatenblatt zur Temperaturkorrektur Temperature Coefficient of Pmax: -0.30 %/°C. Nominal module Operating Temperature (NMOT), Definition: Air mass AM 1.5, irradiance 800 W/m², temperature 20 °C, windspeed 1 m/s. Nominal Module Operating Temperature (NMOT): 44 °C ± 2 °C Reduction in efficiency: From 1000 W/m² to 200 W/m² at 25°C: 3.5 ± 2%. |
I.d.R. wird das Wirkungsgradkennfeld nicht vorliegen. Das vorhandene Kennfeld könnte dann entsprechend skaliert werden (das wird hier nicht gezeigt). Das übliche Vorgehen wird sein, die vom Modulhersteller gemachten Angaben aus dem Datenblatt direkt in einem linearen Modell zu nutzen. Der Wirkungsgrad wird kleiner bei heißen Modulen und bei wenig Solarstrahlung.
Diese Darstellung der Gleichung versucht nicht zu formal zu sein. Werte aus dem Moduldatenblatt werden direkt als Konstanten in die Gleichung eingesetzt. Der Temperaturkoeffizient (-0.30 %/°C) wird als "0,003" eingesetzt. Die Abhängigkeit von der Leistung (3.5 %) wird als "0,035" eingesetzt. TSTC = 25 °C und GSTC = 1000 W/m2.
ηMOD,T,G ist der Wirkungsgrad zur Temperatur und zur Globalstrahlung. Die Leistung wird hier ausgedrückt durch die Einstrahlung auf die geneigte Fläche, Gt (in W/m2). Entsprechend sind die Parameter TMOD und Gt auch die Eingangsparameter in die Gleichung.
Im Planungsstadium muss die Modultemperatur, TMOD berechnet werden. Siehe dazu hier. TMOD ist abhängig von Gt (im WWW: E) und der Umgebungstemperatur (ambient temperature), Tamb .
Die Umgebungstemperatur (ambient temperature), Ta ist für eine einfache Rechnung ohne PV-Simulation ist eine durchschnittliche Tagestemperatur im Sommer um die Mittagszeit – also zu der Zeit in der die PV-Anlage die meisten Erträge erwirtschaftet. Temperaturen gibt es vom DWD (Auswahl z.B.: Temperatur, Mittel/Summen, brd_mpa_1961-1990, Juni). Für Hamburg: 15 °C.
Die Strahlungssumme auf eine horizontale Fläche ist GHI = 1000 kWh/m2 (pro Jahr). Nur Zeiten mit Tageslicht berücksichtigt: 1 Jahr = 365·12 h = 4380 h. Daher ist eine durchschnittliche Globalstrahlung G = 228 W/m2. Im Sommer, um die Mittagszeit auf der geneigten Fläche (dort etwas mehr als horizontal) dann eine geschätzte durchschnittliche Strahlungssumme, Gt,av = 500 W/m2.
Mit der Zusatzinfo zur Temperaturberechnung ergibt sich TMOD = 29,5 °C. Damit (nach einigen kleinen Zwischenrechnungen): ηMOD,T,G = 0,965.
Die Deutsche Gesellschaft fü Solartechnik gibt in ihrem Ordner Verluste an von 3 % bis 9 % im Beispiel: 5 %. Das wäre ein ηMOD,T,G = 0,95.
Interpretation: ηMOD,T,G ist der Einzelwirkungsgrad, der unter allen Verlustursachen den höchsten Effekt hat, gefolgt von der Reflexion am Glas der Module. Der Wirkungsgrad wird kleiner bei heißen Modulen und bei wenig Solarstrahlung. In extremer Ausprägung kommt beides zum Glück nicht gleichzeitig vor. Schwache Strahlung produziert nicht die höchsten Modultemperaturen. Schwache Strahlung führt absolut zu wenig Energieausbeute, da macht sich ein schlechter Wirkungsgrad absolut wenig bemerkbar. Bei einer angenommenen Modultemperatur von 70 °C liefert der Temperatursummand (in der Gleichung für ηMOD,T,G) einen Verlust von 0,003·(70-25)°C = 13,5 %. Der Strahlungssummand kommt "nur" auf maximal auf 0,036·(1000-200)/800 = 3,5 % Verlust. Bei noch weniger Strahlung würde der Wirkungsgrad noch schlechter, aber es wäre sowieso keine Energieausbeute möglich. Das Intervall 3 % bis 9 % der DGS für diesen Teilwirkungsgrad ist also nachvollziehbar. 9 % Verlust werden aber in Deutschland wohl nicht im Jahresmittel erreicht werden.
Wirkungsgrad zur Berücksichtigung verschiedener Verluste an den Solarmodulen, ηMOD,misc
Die Verluste, aus denen der Wirkungsgrad berechnet wird sind hier gegeben. Die Basisinformation zu den einzelnen Verlusten ist von NREL (Archiv) und aus der Hilfe zum Programm PVWatts.
Verschiedene Verluste an den Solarmodulen Standardwert Anmerkungen ------------------------------------------------------------------------------------------------------------------------------- Serienstreuung (nameplate rating) 1,0 % PVWatts Manual Version 5 Anfängliche Degradation (initial degradation) 1,0 % Anfangszeit angeben! Degradation (degradation) 0,5 % p.a. * nach der Anfangszeit Verschmutzung (soiling) 2,0 % PVWatts Manual Version 5 (DGS: 1,0%...3,0%, MW: 1,5%)** Alterung (aging) 0,0 % keine Daten vorhanden Verschattung (shading) 0,0 % Abschätzung oder Simulation (DGS: 0,0%...5,0%, MW: 2,5%) Schnee und Reif (snow and frost) 1,0 % siehe Gleichung unten Reflexion (reflection) 3,8 % siehe Gleichung unten (DGS: 2,5%...5,0%, MW: 3,5%) Mismatching 2,0 % PVWatts Manual Version 5 (DGS: 0,5%...2,5%, MW: 1,5%) ---------------------------------------------------------------- Alles zusammen, Standard (nach Gleichung) 10,4 % * * Die Degradation wird nur in die Finanzanalyse einbezogen Alles zusammen, Standard (Addition, falsch!) 10,8 % * ** DGS, MW: Mittelwert, DGS-Auswahl |
Serienstreuung (nameplate rating):
Die Serienstreuung zeigt die Genauigkeit der Leistungsangabe des Herstellers.
Feldmessungen der Anlage können ergeben, dass die Leistung von der Nennleistung auf dem Typenschild abweicht.
Anfängliche Degradation (initial degradation, light-induced degradation, LID):
In den ersten Betriebstagen kommt es zu einer Verringerung der Leistung der Module.
Dies ist die
lichtinduzierte Degradation (LID) –
ein Phänomen,
bei dem die Leistungsabgabe eines Moduls abnimmt, wenn es zum ersten Mal dem Sonnenlicht ausgesetzt wird.
Abhängig vom Material der Solarzellen beträgt die lichtinduzierte Degradation 1 % bis 2 %.
Dazu sind im Moduldatenblatt Angaben enthalten.
In den folgenden Jahren kommt es dann zur typischen langfristigen Degradation, die geringer ist als die anfängliche Degradation (siehe unten).
"Eine besonders hohe Degradation von bis zu 25 Prozent kann bei Solarzellen aus amorphem Silizium im ersten Betriebsjahr auftreten. Für Solarmodule aus diesem[!] Material wird jedoch nicht die Leistung zu Beginn der Lebenszeit, sondern die Leistung nach der Alterung in den Datenblättern und beim Verkauf angegeben. Solarmodule aus diesem Material haben also zunächst eine höhere Leistung als die, für die man bezahlt hat." Die Degradation erfolgt durch Lichteinstrahlung (Staebler-Wronski-Effekt).
Degradation (degradation):
Unter dem Begriff
Degradation
wird die alterungsbedingte Änderung der Parameter von Halbleiterbauteilen verstanden.
Dazu sind im Moduldatenblatt Angaben und Herstellergarantien enthalten.
Oft wird die Degradation mit 0,5 % pro Jahr angegeben.
Kiefer
(2018, Archiv)
berichtet hingegen von Messungen an Solarmodulen nach einem Betrieb zwischen 8 und 12 Jahren.
Danach beträgt die Degradation durchschnittlich nur 0,14 % pro Jahr, was unterhalb der garantierten Reproduktion der Messung liegt.
Anlagendegradation setzt sich aus allen Ursachen zusammen, die den Ertrag der PV-Anlage gegenüber dem Vorjahr reduzieren. Dies im Unterschied zur "Degradation", die sich nur auf Halbleiterbauteilen im Solarmodul bezieht. Kiefer (2018) berichtet weiter über eine Zunahme der Globalstrahlung auf die geneigte Fläche, Gt um 1,1 % pro Jahr und eine Verringerung der Performance Ratio, PR (die alle Ursachen umfasst) von 0,7 % pro Jahr, Damit bleibt die Anrechnung einer – genauer bezeichneten – "Anlagendegradation" von 0,5 % pro Jahr in einer Finanzanalyse gerechtfertigt.
Spannungsinduzierte Degradation (potential-induced degradation, PID) wird bei kristallinen PV-Modulen hervorgerufen durch sogenannte Leckströme und kann Leistungsverluste von bis zu 30 % verursachen. PID kann verhindert werden, "indem ein Wechselrichter mit der Möglichkeit zur Erdung des positiven oder negativen Poles verwendet wird. Welcher Generatorpol geerdet werden muss, ist mit dem Modulhersteller abzuklären."
Verschmutzung (soiling):
Es handelt sich um Verluste durch Schmutz auf der Oberfläche des PV-Moduls, die verhindern, dass die Sonnenstrahlung die Zellen erreicht.
Verschmutzungen
sind orts- und witterungsabhängig.
"In Gebieten mit hohem Verkehrsaufkommen, hoher Schadstoffbelastung, staubigen Böden und seltenen Niederschlägen kommt es zu größeren Verschmutzungsverlusten.
Verschmutzung kann eintreten durch Laubabwurf, Vogelkot, Staub von Baustellen oder aus der Landwirtschaft, Ruß aus nahen Schornsteinen,
durch regionale Effekte wie Pollenflug oder überregionale Effekte wie Saharastaub-Ereignisse."
(Fraunhofer 2023,
Archiv).
Intensiver Regen wird die Module mit einem optimalen Neigungswinkel größtenteils wieder reinigen.
Weniger gut geht das bei Modulen mit sehr flacher Neigung (unter 15°).
Über die Jahre nimmt allerdings die feste Verschmutzung zu, die vom Regen nicht mehr abgewaschen werden kann (siehe Alterung).
Die Verluste (in Prozent) durch Verschmutzung werden verstanden als die mittlere Verschmutzung
zwischen zwei starken Regenereignissen oder zwischen zwei (schnellen) Putzeinsätzen.
Alterung (aging):
Zu unterscheiden ist zwischen Alterung und Verschmutzung.
Verschmutzung wird vom Regen abgewaschen oder kann leicht entfernt werden.
Alterung sind festere Verschmutzung, die nicht vom Regen abgewaschen werden und nur
unter erheblichem Aufwand beseitigt werden können.
Die Grenze zwischen Alterung und Verschmutzung ist fließend.
Die Verluste (in Prozent) durch Alterung werden verstanden als die irreversible Alterung plus der zusätzlichen mittleren Alterung
zwischen zwei Putzeinsätzen, die mit erheblichem Aufwand durchgeführt werden.
Auf den Modulen kann sich unter Umständen sogenannter Günbelag bilden. Das sind pflanzliche Mikroorganismen – in fortgeschrittenem Stadium zusammen mit Algen, Moosen und Flechten. Grünbelag tritt eher auf bei Teilabschattung der Module. Der Belag tritt eher an der unteren Kante und insbesondere an den unteren Ecken der Module auf. Wegen der Serienverbindung der Solarzellen können stark verschmutzte Teilflächen erheblich stärkere Ertragseinbußen verursachen als es ihrem Flächenanteil entspricht. Grünbelag kann entfernt werden.
Hagel (Archiv) kann Mikrorisse auf der Oberfläche des Moduls verursachen. Eine Beschädigung der Dichtung des Panels kann dazu führen, dass Wasser ins Innere gelangt. Unter bestimmten Wetterbedingungen kann das Wasser verdunsten und sich innen am Deckglas niederschlagen, was die Lichtdurchlässigkeit des Glases verringert. Irreversibel ist eine Vergilbung des polymeren Einbettungsmaterials.
Verschattung (shading):
Reduzierung der einfallenden Sonnenstrahlung durch
Solar-Simulationsprogramme sollten eine Verschattungsanalyse beinhalten. Wenn das der Fall ist, dann kann der pauschale Verlust hier den Wert 0 % erhalten. Wenn kein Solar-Simulationsprogramm verfügbar ist mit einer Verschattungsanalyse, dann kann PVGIS automatisch einen Horizont am Standort erzeugen. Der Effekt der Verschattung wird aus Daten zur Bodenhöhe berechnet. Schatten von sehr nahe gelegenen Objekten wie Häusern oder Bäumen werden dabei nicht berücksichtigt. Alternativ kann ein Horizontdiagramm mit einem "horizon file" eingelesen werden, das auch die nahe gelegenen Objekte enthält.
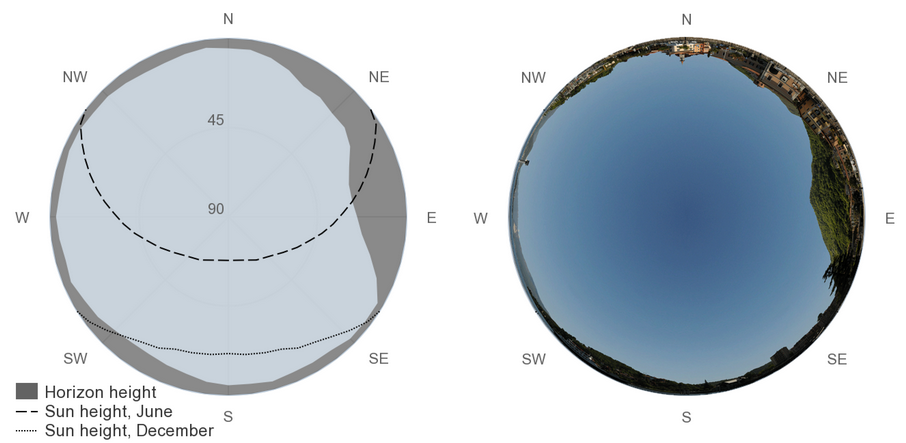
Links: Ein Beispiel des Horizontdiagramms in PVGIS. Rechts: Bild einer Kamera mit Fisheye vom gleichen Standort.
Quelle: PVIS, 2023: PVGIS User Manual. https://joint-research-centre.ec.europa.eu (Archiv)
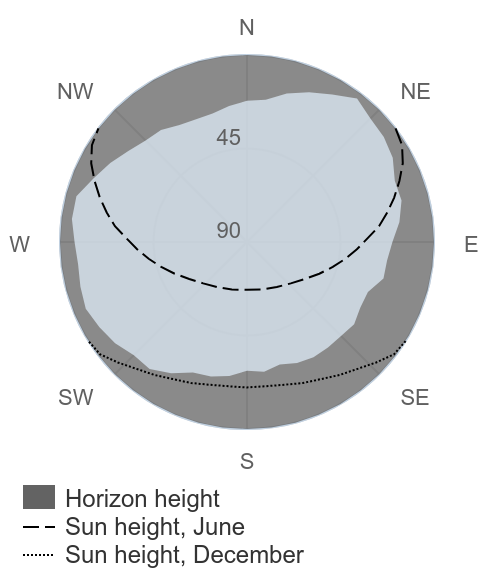

"Chalet 1802" in Chamonix-Mont-Blanc, Frankreich (1050 m, ϕ = 45,9°).
Blick nach Süden zum Mont-Blanc-Massiv (4810 m), Entfernung: 7,4 km, Winkel zum Gipfel: 27° = arctan(3,76/7,4).
Sonnenstand: 21°. Am 21. Dezember geht die Sonne hier nicht auf.
Horizontdiagramm erzeugt mit PVGIS
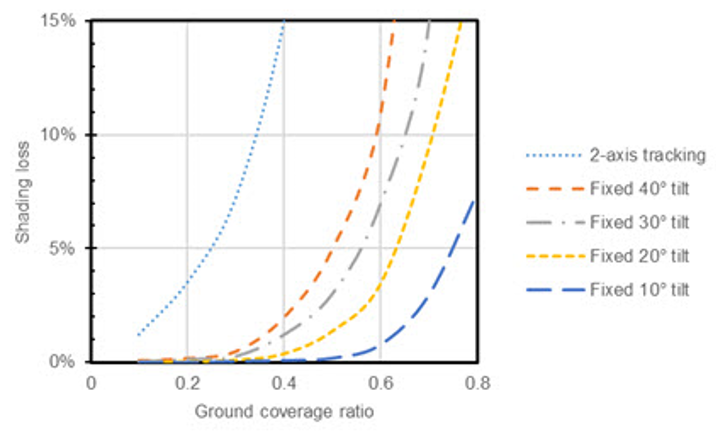
Verschattungsverlust abhängig vom Bodenbedeckungsverhältnis (ground cover ratio, GCR)
für verschiedene Neigungswinkel bei einem Breitengrad von etwa 35 Grad Nord.
Größere Verluste bei einem Standort weiter nördlich.
Quelle: NREL, 2023: PVWatts > Help. https://pvwatts.nrel.gov/pvwatts.php.
Mit der Grafik kann der prozentuale Selbstverschattungsverlust abgeschätzt werden. Eingangsparameter ist das Bodenbedeckungsverhältnis (GCR). Der GCR ist definiert als das Verhältnis der Modul-Fläche zur von der PV-Anlage eingenommenen Boden- oder Dachfläche.
Schnee und Reif (snow and frost):
Es geht um die Reduzierung der Jahresleistung der Anlage aufgrund einer Schneedecke auf der Anlage oder einem Reifüberzug.
Nach DWD haben wir in Norddeutschland in den letzten 11 Jahren 1,5 Monate (1,5/12 = 12,5 %) mit Schnee gehabt. Dazu die Karte von 2022/2023.
Beispiel: In den Monaten Dez./Jan./Feb. liefert eine PV-Anlage 8,6 % des Jahresertrages. Das macht zusammen einen Verlust durch Schnee von 12,5 % · 8,6 % = 1 %. |
Der Schnee wird teilweise von den Modulen von selbst abrutschen. Der Verlust wäre 0 %, wenn die Module per Hand schneefrei gehalten werden. Alternativ können in einer Simulation monatlich reduzierte Einstrahlungswerte verwendet werden, um die Verluste durch Schnee und Reif darzustellen, anstatt Schnee und Reif pauschal als Prozentwert einzubeziehen.
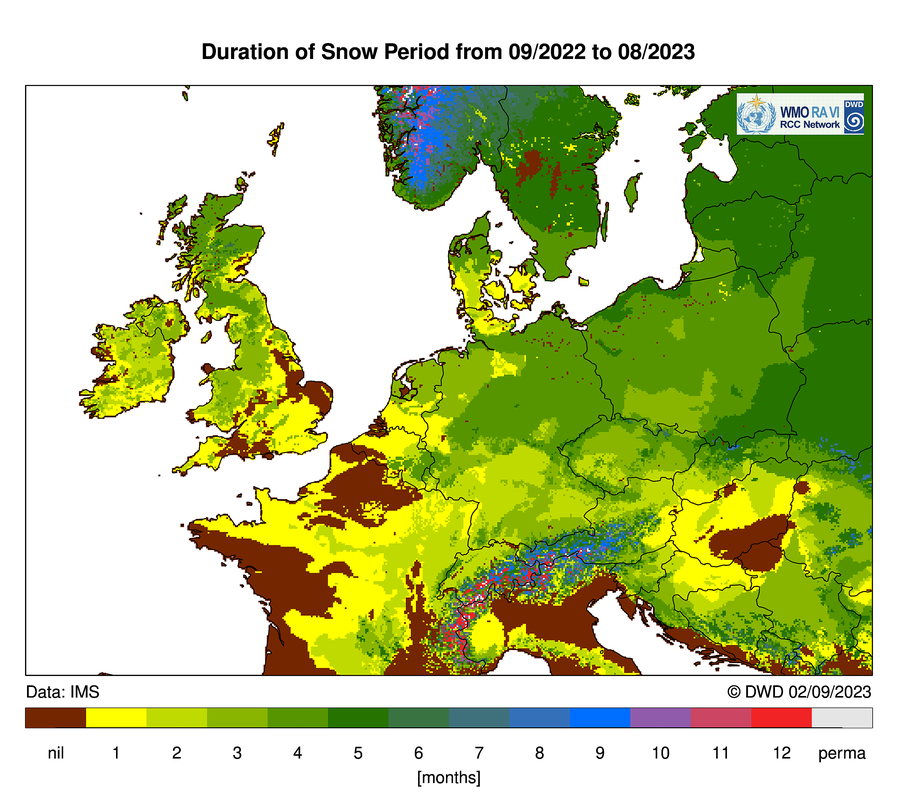
Dauer der Schneeperiode von 09/2022 bis 08/2023 in Zentraleuropa. Für Hamburg werden 2,5 Monate genannt.
Quelle: DWD, 2023: Klimakarten Europa, Schnee, Jahreswerte.
Reflexion (reflection):
Der Anteil des von einem Moduls reflektierten Lichts hängt vom Einfallwinkel, θ des Lichts ab.
Je größer der Einfallwinkel, desto größer ist der reflektierte Anteil.
Der Einfallwinkeleffekt (incidence effect, designated term: Incidence Angle Modifier, IAM) ist definiert als das Verhältnis von Licht,
das bei einem bestimmten Einfallwinkel durchgelassen wird, zum durchgelassenen Licht bei senkrechtem Einfall.
Es handelt sich um ein allgemeines physikalisches Phänomen.
Die Reflexionsverluste entstehen hauptsächlich an der Glasabdeckung.
Reflexion und Transmission des Sonnenstrahls findet an jeder Materialschnittstelle statt.
Die Schnittstellen sind: Luft-Glas, Glas-EVA, EVA-Solarzelle. EVA ist Ethylenvinylacetat zum Schutz der Solarzelle.
Im Glas gibt es eine gewisse Absorption. Dies ergibt sich für jeden einfallenden Strahl.
Bei senkrechtem Einfall liegt die Reflexion in der Größenordnung von 5 % und
ist in der gemessenen Leistung unter Standard Test Conditions (STC) bereits enthalten.
Der IAM betrifft nur die Winkelabhängigkeit dieses Effekts, d. h.
es wird auf die Transmission bei senkrechtem Einfall (Einfallwinkel 0°) normiert.
Die IAM-Korrektur sollte in Solar-Simulationsprogrammen in jedem Schritt berücksichtigt werden.
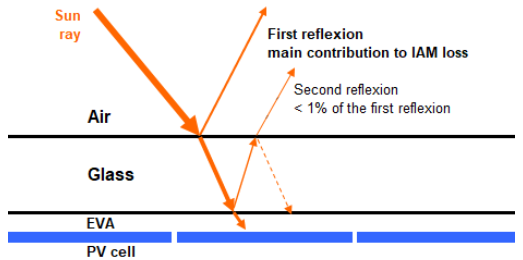
Transmission und Reflexion der Solarstrahlung an einem Solarmodul.
Quelle: PVsyst, 2023: Help > Project design > Array and system losses > Array incidence loss (IAM).
https://www.pvsyst.com/help.
(Archiv)
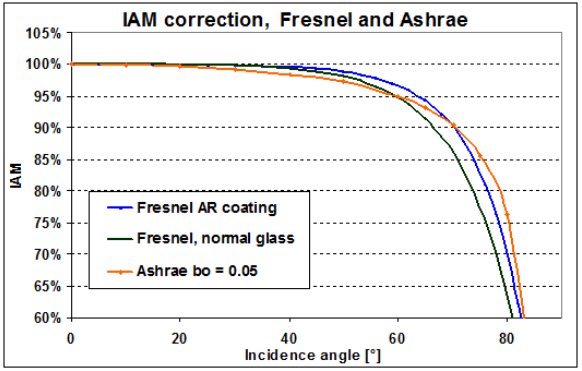
Korrekturfaktor (Wirkungsgrad) für den Durchgang der Strahlung durch das Glas des Solarmoduls.
Quelle: PVsyst, 2023: Help > Project design > Array and system losses > Array incidence loss (IAM).
https://www.pvsyst.com/help.
(Archiv)
.
Der Effekt des IAM im Betrieb einer PV-Anlage über ein ganzes Jahr muss pauschal abgeschätzt werden, wenn ein Solar-Simulationsprogramme die Reflexion nicht berücksichtigt oder wenn eine einfache Abschätzung ohne Simulationsprogramm gemacht werden soll.
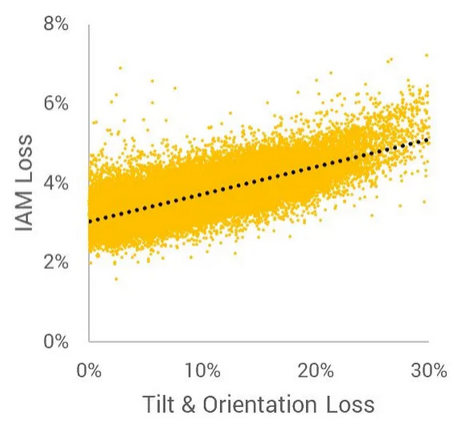
Durch Abweichungen des Einfallwinkels von der senkrechten: Reflexionsverluste einer Solaranlage nach längerem Betrieb.
Quelle: AuroraSolar, 2023: Panel Angle & Orientation. In: The Ultimate Guide to PV System Losses (eBook).
https://resources.aurorasolar.com/pv-system-losses-ebook.
(Archiv)
.
Ht,rel wird abgelesen aus dem Anlagenkennfeld für Anlagenkennfeld für Hamburg/Berlin/München (siehe oben) und als z.B. 0,871 (für β = 0°) in die Gleichung für LIAM eingesetzt: 6,5 % ·(1 – 0,871) + 3 % = 3,8 % .
Mismatching
Zwei Module des gleichen Typs vom gleichen Hersteller sind nicht vollkommen identisch.
Herstellungsunterschiede führen zu kleinen Abweichungen in den elektrischen Parametern der Module.
Mismatching ist auf diese Herstellungsschwankungen zurückzuführen,
weil der Maxium Power Point Tracker (MPPT) nicht für jedes Modul den MPP finden kann.
Verluste werden minimiert bei Verwendung von Mikrowechselrichtern oder DC-Optimierern,
da diese Leistungselektronik auf Modulebene die Module voneinander isoliert.
Der Wechselrichterwirkungsgrad (Archiv) besteht im Wesentlichen aus dem Wechselrichter-Umwandlungswirkungsgrad, der durch die Wirkungsgradkennlinie des Wechselrichters gegeben ist. Hinzu kommen noch diverse kleinere Effekte, die als Verluste separat erfasst werden und im Wirkungsgrad zur Berücksichtigung verschiedener Verluste am Wechselrichter zusammengefasst werden. Der Wechselrichter-Umwandlungswirkungsgrad wird zwischen Eingang und Ausgang des Wechselrichters definiert. Weitere verschiedene Verluste (miscellaneous losses) werden in einem "virtuellen Kasten" dem Wechselrichter separat, nachgeschaltet gedacht. Dies genau so, wie bei den Systemwirkungsgraden (system efficiencies) – siehe unten –, die auch Verluste kennzeichnen, die sich irgendwo zwischen den Hauptkomponenten befinden.
Wechselrichter-Umwandlungswirkungsgrad, ηINV,conv
PAC: Wechselstromleistung am Ausgang des Wechselrichters
PDC: Gleichstromleistung am Eingang des Wechselrichters
PL: Leistungsverlust (power loss) im Wechselrichter
Umwandlungsverluste im Wechselrichter entstehen insbesondere in seinem Leistungsteil durch Leistungstransistoren und andere Bauteile. Heute werden trafolose Wechselrichter gebaut. In älteren Wechselrichtern waren Transformatoren verbaut, die zu weiteren Verlusten führten.
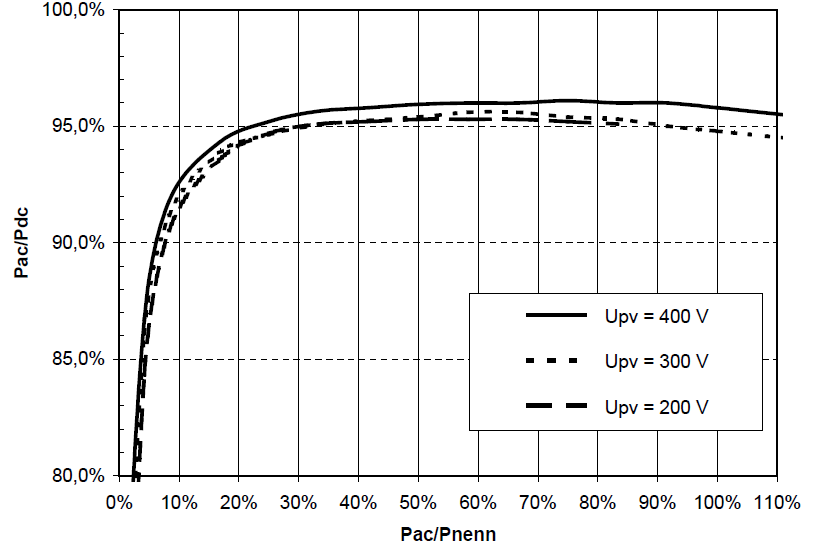
Kennlinie des Wechselrichters SMA Sunny Boy 2000 aus dem Jahr 2001.
Heute sind die Wirkungsgrade von Wechselrichtern deutlich höher.
Der Wirkungsgrad ist abhängig von der relativen Leistungsentnahme und von der Eingangsspannung in den Wechselrichter.
Bei hohen Eingangsspannungen erreichen Wechselrichter einen etwas höheren Wirkungsgrad.
ηmax: 96,0 %, ηEU: 95,3 % bei 400 V.
Quelle: SMA, 2001: Sunny Boy 2000 – Technische Beschreibung.
Eine Wechselrichterkennlinie kann mit diesen Gleichungen beschrieben werden:
.
Leerlaufleistung (no-load power), P0
Blindspannung (reactive voltage), Ur
Innenwiderstand (internal resistance), Ri
Die Werte 6 W, 4 V und 0,75 Ω gelten für einen Wechselrichter mit einer Nennleistung von 1 kW. Diese Nennleistung wurde als "Standardnennleistung" gewählt zur Definition der Parameter. Die 4. Zeile mit drei Gleichung (oben) zeigt, wie diese Werte auf andere Nennleistungen des Wechselrichters, PAC,INV umgerechnet werden können.
|
Beispiel
Die Parameter P0, Ur und Ri sollen von den Standardwerten (bei 1 kW) 6 W, 4 V und 0,75 Ω umgerechnet werden auf einen Wechselrichter mit einer Nennleistung, PAC,INV von 10 kW.
Je nach Parameter müssen wir den Faktor 10, 1 oder 1/10 nutzen: |
Eine Umrechnung ist entbehrlich, denn wenn erst einmal eine Wechselrichterkennlinie vorliegt (erzeugt für 1 kW), dann kann diese (dimensionslose) Kennlinie für Wechselrichter jeder Größe übernommen werden. Wenn die Werte skaliert werden, dann bleibt die Wechselrichterkennlinie die gleiche und ebenso der maximale Wirkungsgrad ηINV,max.
Eine Kennlinie mit den hier gegebenen Werten hat einen maximalen Wirkungsgrad, ηINV,max = 96,7 % und einen EU-Wirkungsgrad, ηEU = 96,1 % (siehe unten).
Wirkleistungsbegrenzung (clipping) kann sich ergeben, wenn die Nennleistung der Solarmodule, PDC,MOD größer ist als die Nennleistung des Wechselrichters, PAC,INV. Die Ausgangsleistung des Wechselrichters ist auf die Nennleistung, PAC,INV beschränkt. Eine Eingangsleistung, die theoretisch (!) zu einer relativen Ausgangsleistung PAC / PAC,INV > 1 führen würde, wird auf PAC,INV beschränkt. Das wird Wirkleistungsbegrenzung (clipping) genannt. Der Wirkungsgrad verringert sich dann stark mit zunehmender zugeführter Leistung – ausgedrückt durch eine theoretische (!) relative Ausgangsleistung größer als 1. Begründung: Wird dem Wechselrichter zunehmend mehr Leistung zugeführt als die Nennleistung, dann wird die Ausgangsleistung auf die Nennleistung des Wechselrichters, PAC,INV beschränkt. Die Ausgangsleistung ist dann wegen der Wirkleistungsbegrenzung konstant, während die Eingangsleistung weiter steigt. Das verringert den Wirkungsgrad, weil das Verhältnis von Ausgangsleistung zu Eingangsleistung bei steigender Eingangsleistung sinkt. Der Wirkungsgrad verringert sich stark mit zunehmend zugeführter Leistung. Daher müssen Solarmodule und Wechselrichter in ihrer Nennleistung aufeinander abgestimmt sein. Bekannt ist, dass Solarmodule ihre Nennleistung, PSTC fast nie erreichen. Daher wäre eine Idee, die Module mit einem Wechselrichter einer kleineren Nennleistung zu kombinieren. Ein kleinerer Wechselrichter ist preiswerter. So könnte man Geld sparen. Wird der Wechselrichter aber kleiner dimensioniert, dann werden einzelne Leistungsspitzen abgeschnitten. Das Bild zeigt, was ein Clipping für den Wirkungsgrad des Wechselrichters bedeutet. Fazit: Module und Wechselrichter sollten ähnliche Nennleistung haben. Mehr zum Thema weiter unten im Abschnitt "Wirkleistungsbegrenzung".
Jahreswirkungsgrad eines Wechselrichters ist der Wirkungsgrad, der sich im Mittel während des Betriebs über einem Jahr ergibt. Die PV-Anlage wird während des Jahres mit verschiedenen relativen Leistungen, PAC / PAC,INV betrieben. Hier im Bild ein Beispiel. Die relative Leistung von 0 % bis 100 % ist in 40 Intervalle eingeteilt, mit einer Breite von je 2,5 %. Sowohl die Zeit – die Häufigkeit –, die der Wechselrichter in jedem Intervall zubringt wird gezählt, als auch die Energie, die in jedem Intervall angeboten und genutzt wird. Durch die Auslegung mit DF = PSTC / PAC,INV = 1 wird (fast) keine Energie vom Wechselrichter abgeschnitten (kein Clipping), weil ein Energieangebot PDC / ηINV,conv > PAC,INV äußerst selten ist und (wenn überhaupt) nur sehr kurz auftritt. Eine Jahres-Simulation mit Stundenwerten kann solche kurzen Ereignisse nicht erfassen. Daher ist es schwierig beim Thema Wirkleistungsbegrenzung zu belastbaren Aussagen zu kommen. Mehr weiter unten im Abschnitt "Wirkleistungsbegrenzung".
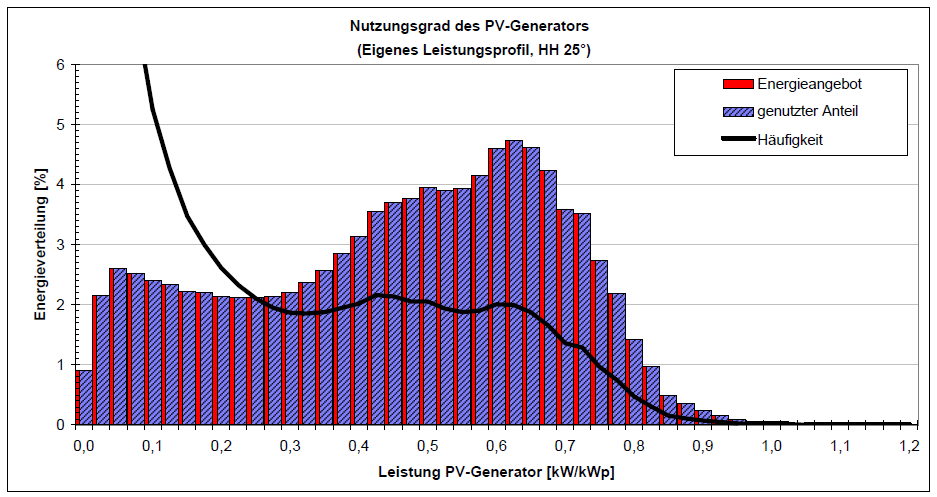
Oben: Das Kennfeld mit der solaren Energie eines Jahres verteilt über verschiedene Leistungsbereiche bereitgestellt von einem Wechselrichter
SMA Sunny Boy 2000 aus dem Jahr 2001.
Dimensionierungsfaktor, DF = PSTC / PAC,INV = 1.
Erstellt mit: SMA, Excel-Tabelle GenAu 5.3 ("GeneratorAuslegung") zur Planung von PV-Anlagen hinsichtlich der Kombination von Modulen und Wechselrichter.
Unten: Energieverteilung im Europäischen Wirkungsgrad.
Wenig Übereinstimmung mit der Energieverteilung in Deutschland nach SMA-Berechnung.
Aus dem Bild (oberer Teil) ist ersichtlich, dass ein Wechselrichter (in Deutschland) oft im Teillastbereich genutzt wird, wegen der geringen Solarstrahlung in den Wintermonaten und wegen vieler Wolken. Dem oberen Diagramm kann man ein Maximum des Energieangebotes bei 0,65 der relativen Nennleistung von Solarmodulen und Wechselrichter entnehmen. Daher ist wichtig, dass der maximale Wirkungsgrad des Wechselrichters in diesem Bereich liegt. Weiterhin ist wichtig, dass die Wirkungsgradkurve nicht links und rechts von 0,65 der relativen Leistung zu stark einbricht. Ein gewichteter Wirkungsgrad, der mehrere Punkte der Wirkungsgradkennline in den Blick nimmt hilft weiter.
Der Europäische Wirkungsgrad ist ein gewichteter Wirkungsgrad. Ziel ist, neben dem Volllastbereich auch den Teillastbereich zu erfassen und dies als eine Zahl anzugeben. Der Europäische Wirkungsgrad ist in DIN EN 50524 genormt. Die Definition lautet
.
η5% ist dabei der Wirkungsgrad bei einer relativen Leistungsentnahme vom 5 % . Entsprechend so auch bei den anderen Prozent-Angaben. ηEU hat die stärkste Gewichtung bei 50% relativer Leistungsentnahme mit einem Gewichtungsfaktor von 0,48. Ein Hersteller wird einen Wechselrichter nach dem EU-Wirkungsgrad also so bauen, dass der maximale Wirkungsgrad bei etwa 50% relativer Leistungsentnahme liegt und links und rechts davon möglichst wenig abfällt.
Das Datenblatt eines Wechselrichters enthält eine Angabe zum maximalen Wirkungsgrad und eine zum EU-Wirkungsgrad. Aus diesen zwei Angaben kann mit einigem Aufwand auch eine Kennlinie rekonstruiert werden. Dazu später mehr.
Beispiel: SMA Sunny Tripower CORE2, STP 110-6, PAC,INV = 110 kW Maximaler Wirkungsgrad, ηINV,max: 98,6 % Europäischer Wirkungsgrad, ηEU: 98,4 % Eigenverbrauch (Nacht): < 5 W |
Wenn für eine einfache Rechnung nur ein Wirkungsgrad für den Wechselrichter herangezogen wird, dann soll es der Europäischer Wirkungsgrad, ηEU sein (nicht der maximale Wirkungsgrad).
Wenn der Europäischer Wirkungsgrad nur unwesentlich unter dem maximaler Wirkungsgrad liegt, dann deutet das auf einen guten Wirkungsgrad auch im Teillastbereich hin. Allerdings weisen selbst alte Wechselrichter nur diese kleine Differenz auf zwischen maximalen Wirkungsgrad und EU-Wirkungsgrad. Die Bedeutung des Europäischer Wirkungsgrades darf also für die Planung von PV-Anlagen nicht überschätzt werden. Wechselrichter sind heute mit sehr guten Wirkungsgraden ausgestattet. Umfangreiche weitere Überlegungen sind an dieser Stelle entbehrlich. Dies insbesondere im Vergleich mit den vielen anderen Wirkungsgraden (und Verlusten), die ansonsten auch noch bei einer PV-Anlage betrachtet werden müssen und zusammen um eine Zehnerpotenz größer sind. Der Europäischer Wirkungsgrad ist trotzdem einen Blick wert beim Kauf eines Wechselrichters.
Wirkungsgrad zur Berücksichtigung verschiedener Verluste am Wechselrichter, ηINV,misc
Verschiedene Verluste am Wechselrichter Standardwert Anmerkungen ------------------------------------------------------------------------------------------------------------------------------------------- Maximum Power Point Tracking (MPPT) 0,5 % Schätzung (DGS: 0,5%...3,0%, MW: 0,7%) Wirkleistungsbegrenzung (clipping) 0,2 % für PDC,MOD / PAC,INV = 1. Sonst: siehe Diagramm Nachtverbrauch (night consumption) 0,2 % Rechnung (s.u.) Eingangsleistungsschwelle (power threshold) 0,1 % Schätzung (s.u.) ---------------------------------------------------------------- Alles zusammen, Standard (nach Gleichung) 1,0 % = LINV,misc |
Maximum Power Point Tracking (MPPT)
Verluste beim
MPP-Tracking
entstehen dadurch, dass der
Wechselrichter
eine gewisse Zeit benötigen, um den korrekten Maximum Power Point (MPP) zu finden oder
daher, dass es eine Differenz zwischen Arbeitspunkt und dem wirklichen MPP bestehen bleibt.
Schnelles MPP-Tracking sorgt also dafür, dass auch kurzzeitige Einstrahlungsspitzen,
wie sie an Tagen mit wechselnder Bewölkung auftreten, genutzt werden.
Verluste beim MPP-Tracking hängen ab vom jeweiligen MPP-Algorithmus und der Variabilität der Bestrahlungsstärke.
Diese Variabilität kann in einer PV-Simulationsrechnung natürlich nicht erfasst werden, wenn
Wetter- und Strahlungsdaten nur stündlich vorliegen.
MPPT-Anpassungsverluste sind etwas anderes als Mismatching. Beim Mismatching geht es um die Unmöglichkeit zwei unterschiedliche Module mit einem MPP-Tracker optimal zu versorgen.
Der MPP ist die optimale Kombination aus Spannung und Stromstärke im Modul, so dass mit P = U · I die höchste mögliche Leistung entnommen wird. Ein Wirkungsgrad, ηMPPT wird zwar gefordert, ist aber nicht verfügbar. Die Verluste werden (vorerst) mit 0,5 % geschätzt. Das Bild zeigt die hohe Variabilität der Leistung bei teilweise bewölktem Himmel.
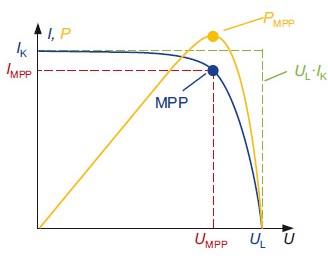
Kennlinie einer Solarzelle. Die Stromstärke, ist als Funktion über der Spannung aufgetragen.
Am Maximum Power Point (MPP) wird die Leistung, PMPP
aus Stromstärke, IMPP multipliziert mit Spannung, UMPP maximal.
Eine Leistung aus Kurzschlussstrom, IK multipliziert mit Leerlaufspannung, UL ist nicht erreichbar.
Die gleiche Kennlinie gilt für ein Solarmodul, wenn dieses aus gleich bestrahlten und identischen Solarzellen besteht.
Quelle: K. Mertens, www.lehrbuch-photovoltaik.de, Bild 4.12.
Die Leistung einer PV-Anlage, PAC wird an einem Tag mit stark unterschiedlicher Bewölkung gemessen.
Mit dieser Variabilität muss der Maximum Power Point Tracker (MPPT) zurecht kommen.
Wirkleistungsbegrenzung (clipping):
Eine Wirkleistungsbegrenzung ist eigentlich nicht gewollt, weil sie Verluste verursacht, die (u.a.) hier berücksichtigt werden müssen.
Gründe für eine Wirkleistungsbegrenzung könnten aber sein:
Eine Wirkleistungsbegrenzung ergibt sich zwischen dem Solarmodul und dem Wechselrichter. Beide müssen von ihrer Nennleistung her aufeinander abgestimmt sein. Heute geht man davon aus, dass es recht optimal ist, wenn Solarmodul und Wechselrichter die gleiche Nennleistung haben. Zur wissenschaftlichen Analyse siehe BURGER, Bruno, 2005. Auslegung und Dimensionierung von Wechselrichtern für netzgekoppelte PV-Anlagen. 20. Symposium Photovoltaische Solarenergie, Bad Staffelstein. https://www.photovoltaikforum.com. (Archiv).
|
|
In Deutschland ist es recht selten, dass eine Einstrahlung unter Standard Test Conditions (STC) in der Praxis einer PV-Anlage erreicht wird. Trotzdem gibt es solche Bedingungen – wenn auch nur im Zeitraum von Minuten. Nach Burger (2005) führt das bei einer Auslegung mit PAC,INV = PDC,MOD = PSTC dann nur noch zu sehr kleinen Verlusten von 0,2 %. Würde man den Wechselrichter größer wählen mit PAC,INV = 1,25·PDC,MOD entsprechend PDC,MOD / PAC,INV = 0,8 , dann würden keine Clipping-Verluste mehr auftreten, dafür würde man den Wechselrichter (Beispiel) statt bei 50 % relativer Leistung jetzt nur noch bei 40 % relativer Leistung fahren und hätte entsprechend einen etwas schlechteren Wirkungsgrad. Diese Überlegungen bestätigen noch einmal die Richtigkeit der einfachen Auslegungsregel.
Die Beurteilung der Auswirkungen einer Wirkleistungsbegrenzung erfordert eine Simulation mit hoher zeitlicher Auflösung von mindestens einer Minute. Hinweise kann das Diagramm liefern.
Verluste durch Wirkleistungsbegrenzung (clipping) bei Wechselrichtern.
Die Verluste wurden berechnet aus dem Jahreswirkungsgrad (L = 1 - η)
als Funktion des Verhältnisses von Solargeneratorleistung, PDC,MOD zur AC-Nennleistung, PAC,INV des Wechselrichters.
Die Berechnung wurde mit "Momentanwerten" durchgeführt (statt gemittelten Stundenwerten).
Dadurch wurden höhere Verluste sichtbar.
Dies am Beispiel einer PV-Anlage in Freiburg im Jahr 2000 bei Schrägdachmontage mit guter Hinterlüftung. PAC,INV = 3 kW.
Nach: BURGER, Bruno, 2005. Auslegung und Dimensionierung von Wechselrichtern für netzgekoppelte PV-Anlagen. 20. Symposium Photovoltaische Solarenergie, Bad Staffelstein.
https://www.photovoltaikforum.com.
(Archiv)
Stand-by- und Nachtverbrauch (night consumption):
Der Wechselrichter ist nie ganz ausgeschaltet. Das Gerät ermittelt während es abgeschaltet ist,
ob die Strahlungsbedingungen ausreichend sind, so dass wieder eingeschaltet werden kann.
Der Verlust kann abgeschätzt werden. Im Datenblatt des Wechselrichters ist der Nachtverbbrauch angegeben.
Situation: Ein Wechselrichter mit 10 kW hat nachts einen Eigenverbrauch von 5 W. Ergebnis: Bei einem spezifischen Jahresertrag von 1000 kWh betragen die Verluste, Lnight 0,22 % Anmerkung: Im Datenblatt zum SMA Sunny Tripower CORE2 (s.o.) ist der Eigenverbrauch (Nacht) nur mit "< 5 W" für einen großen Wechselrichter mit 110 kW angegeben. |
Eingangsleistungsschwelle (power threshold):
Die Eingangsleistungsschwelle ist die Mindestleistung, die am Eingang eines Wechselrichters bereit stehen muss,
bevor der Wechselrichter sich einschalten kann.
Von den Modulen muss etwa das 2-fache der Leerlaufleistung, P0 zur Verfügung stehen für einen Start in den Tag.
Die Leerlaufleistung beträgt etwa 5 W pro 1000 Wp. Das Zweifache sind 10 W oder 1 %.
Das Bild zeigt die Situation einer 1 kWp-Anlage im Juni.
Die Situation ist mit sogar 30 W gezeigt. Die am Tage geerntete Energie ist proportional zur Fläche unter der Kurve:
Gt·t. Am Abend geht von der ganzen Fläche nur das kleine "Dreieck" verloren rechts vom eingezeichneten Strich.
Am Morgen dazu ein gleiches Dreieck. Das ist gegenüber der ganzen Fläche unter der Kurve so gut wie nichts.
Wir setzten als Verlust 0,1 % an – nur um den Posten nicht zu vergessen.
Die Eingangsleistungsschwelle führt nur zu einem verschwindend kleinen Leistungsverlust:
2-mal (morgens und abends) das kleine Dreieck rechts vom eingezeichneten Strich.
Quelle: Erstellt mit PVGIS.
Eine Verfügbarkeit (availability), A kann als entsprechender Wirkungsgrad, ηavail gedeutet werden. Eine fehlende Verfügbarkeit kann dem ganzen PV-Vorhaben einen Strich durch die Rechnung machen. Eine fehlende Verfügbarkeit hat teilweise technische Gründe (Ausfall von Wechselrichtern) und gehört dann zum PV-System. Verzögerungen können aber auch nicht-technische Gründe haben und bleiben bei einer rein technischen Analyse dann unberücksichtigt.
Bei der Planung einer PV-Anlage wird die Verfügbarkeit i.d.R. noch nicht berücksichtig, weil für die Zukunft keine Aussagen über Ausfallzeiten gemacht werden können. Eine konservative Vorgehensweise in der Planung kann aber sicherheitshalber einen statistisch belegten prozentualen Verlust (3 %) berücksichtigen.
Wirkungsgrad zur Berücksichtigung verschiedener Verluste von Komponenten und Umständen im System, ηSYS
Verschiedene Verluste im System Standardwert Anmerkungen --------------------------------------------------------------------------------------------------------------------------------------------- Verkabelung (wiring), DC 0,5 % (DGS: 0,5%...1,5%, MW: 0,8%) Verkabelung (wiring), AC 0,5 % (DGS: 0,2%...1,5%, MW: 0,5%) Stecker (connections) 0,0 % Verlust sehr gering ---------------------------------------------------------------- Alles zusammen, Standard (nach Gleichung) 1,0 % = LSYS Verfügbarkeit (availability) 3,0 % = Lavail Vorschlag aus dem PVWatts Manual Version 5. Siehe Gleichungen unten. |
Verkabelung (wiring):
In aller Kürze ist die Auslegung der Verkabelung von PV-Anlagen
hier
beschrieben. Der Leitungsquerschnitt wird so berechnet, dass ein vorgegebener relativer Leistungsverlust nicht überschritten wird.
Mit diesem Leitungsquerschnitt wird dann der relative Leistungsverlust ausgerechnet.
Theoretisch kommt dann genau der vorgegebene relative Leistungsverlust auch wieder heraus.
In der Praxis wird der Verlust aber immer etwas geringer ausfallen als vorgegeben,
weil Kabelquerschnitte genormt sind und der nächste größere Querschnitt gegenüber dem Rechenergebnis gewählt wird.
Querschnitte sind in gängigen Größen 4,0 mm2, 6,0 mm2, 10,0 mm2, 16,0 mm2 vorhanden.
Die Empfehlung lautet, dass sowohl in den DC-Leitungen wie auch in den AC-Leitungen ein Verlust von 1 % nicht überschritten werden soll.
Es ergibt sich danach in Summe ein maximaler Verlust von 2 %.
Aufgrund der Tatsache, dass oft Kabelquerschnitte größer gewählt werden als erforderlich,
sollte in Summe von DC- und AC-Leitungen als Standardwert: 1 % gewählt werden.
Stecker (connections):
Stecker verursachen einen geringen Zusatzwiderstand. Dieser ist sehr viel geringer als die Verluste in den Kabeln.
Man kann einen Verlust von 0,5 % ansetzen. Das wäre aber schon mehr als tatsächlich auftritt.
Quasi-Standard ist der MC4-Stecker von https://www.staubli.com.
Verfügbarkeit (availability), ηavail
Technische Verfügbarkeit (technical availability) – zeitbasiert (time-based), At wird für PV-Anlagen hier von Solar Best Practices definiert. Es ist ein Begriff aus dem Bereich Betrieb und Wartung (operation and maintenance).
Als nützliche Zeit (useful time), tuseful zählt die Zeit, während der normalerweise Strom erzeugt wird. Das ist die Zeit in der eine ausreichende Strahlung vorliegt zum Betrieb der PV-Anlage. Welche Leistung am Wechselrichter mindestens vorliegen muss, wurde oben zum Thema "Eingangsleistungsschwelle" erklärt. Als Ausfallzeit (downtime), tdown wird nur Zeit angerechnet, die in das Intervall der nützlichen Zeit fällt.
Ausfall bedeutet oft einen Ausfall von Wechselrichtern. Dabei müssen nicht gleich alle Wechselrichter ausfallen. Die Verfügbarkeit jedes Wechselrichters wird separat ausgerechnet (wie oben gezeigt). Die gesamte Verfügbarkeit wird dann gewichtet anhand der Nennleistung der n Wechselrichter oder der Anzahl gleicher Wechselrichter.
Die Verfügbarkeit kann sich auch auf eine bestimmte Zeitspanne beziehen und die Energie, die in dieser Zeit erzeugt wird (oder auch nicht erzeugt wird). Es wird also eine energiebasierte Verfügbarkeit (energy based availability), AE berechnet als
.
E ist die produzierte und gemessene Energie in der definierten Periode (Tag, Monat, Jahr). Eloss ist die durch Ausfall entgangene Energie, die durch eine Simulationsrechnung ermittelt wird.
Es ist fraglich, ob eine Verfügbarkeit überhaupt in die Berechnung eines Wirkungsgrades einer Anlage einbezogen werden soll. Die hier berechnete Verfügbarkeit wurde (oben) technische Verfügbarkeit gekannt. Es geht also um die Gründe für den Ausfall. Ein durch die Technik verursachter Ausfall kann dann durchaus in den Wirkungsgrad einfließen, denn eine Komponente hat nicht nur eine Leistungscharakteristik, sondern auch eine technische Ausfallwahrscheinlichkeit. Wenn die Ausfallwahrscheinlichkeit hoch ist, dann kann dies eben auch in eine umfassende technische Bewertung eingehen.
Die Verfügbarkeit, At bzw. AE kann maximal den Wert 1 annehmen, so wie auch der Wirkungsgrad. Daher ist dann auch
.
Natürlich gibt es auch nicht-technische Gründe für einen Ausfall. Stichworte dazu: Finanzierung, Planung, Genehmigungen, Hersteller, Zwischenhandel, Installateur, Wetter und sicher noch viele mehr.
Anlagenwirkungsgrad (performance ratio), PR:
In einem großen Schritt können jetzt alle weiteren Wirkungsgrade zusammengefasst werden
durch den Anlagenwirkungsgrad, auch: Anlagennutzungsgrad (performance ratio), PR.
Performance Ratio ist die englische Bezeichnung, die auch im deutschen Sprachraum geläufig ist.
Die Bezeichnung Performance Ratio ergibt sich aus der englischen Betrachtung,
bei der zwei spezifische Erträge ins Verhältnis gesetzt werden.
Das erscheint mir wenig intuitiv. Wir bleiben daher gedanklich bei den Wirkungsgraden. PR = ηPR ist dann einfach ein weiterer Wirkungsgrad zwischen PV-Generator bei Standard Test Conditions (STC) und der Übergabe von Leistung oder Energie in das Netz:
,
,
.
Setzt man – wie üblich – den Ausgangspunkt nicht an der Sonne an, sondern beim Eintreffen der Energie auf der geneigten Fläche, dann erhält man die Ausgangsparameter der PV-Anlage sofort mit
.
Die Trennung der Betrachtung zwischen ηMOD,STC und PR findet also mitten im PV-Modul statt. Aus diesem Grund wurden im Bild oben auch zwei Module in einem Kasten gezeigt. Der vergleichsweise niedrige Modulwirkungsgrad bei Standardtestbedingungen ist nicht Teil des Anlagenwirkungsgrades, PR. Die vielen weiteren kleineren Verluste im Solarmodul sind aber alle PR zugeordnet!
Korrigierter Anlagenwirkungsgrad (corrected performance ratio), PRcorr :
Wenn ein Wirkungsgrad – wie PR – zur Leistungsüberwachung eingesetzt werden soll, so stört es,
wenn der Wert mit Änderungen in der Globalstrahlung und der Temperatur der Module schwankt.
Dies sind Parameter, die von außen gegeben sind und nicht vom Betrieb der Anlage abhängen.
Nach Abtrennen des Temperatur- und Globalstrahlungswirkungsgrad, ηMOD,T,G bleibt ein
korrigierter Anlagenwirkungsgrad (corrected performance ratio), PRcorr übrig,
der sich nicht mehr mit der Temperatur der Module stark ändert.
PRcorr ist daher besser zur Anlagenüberwachung geeignet.
Geht es um einen momentanen Betriebszustand und die zugehörigen Leistungen, so kann PR einfach zu PRcorr korrigiert werden. Wenn sich PR aber aus einer Energiebetrachtung ergibt, dann muss zur Korrektur (also zur Abtrennung des Temperatur- und Leistungswirkungsgrades) das ganze Zeitintervall (nach)simuliert werden. Das erfordert entsprechende Software und ist daher aufwändig. PRcorr ist daher ein Parameter, der für den einfachen Anlagenbetrieb nicht geeignet ist.
Die Textboxen am Anfang der Abschnitte
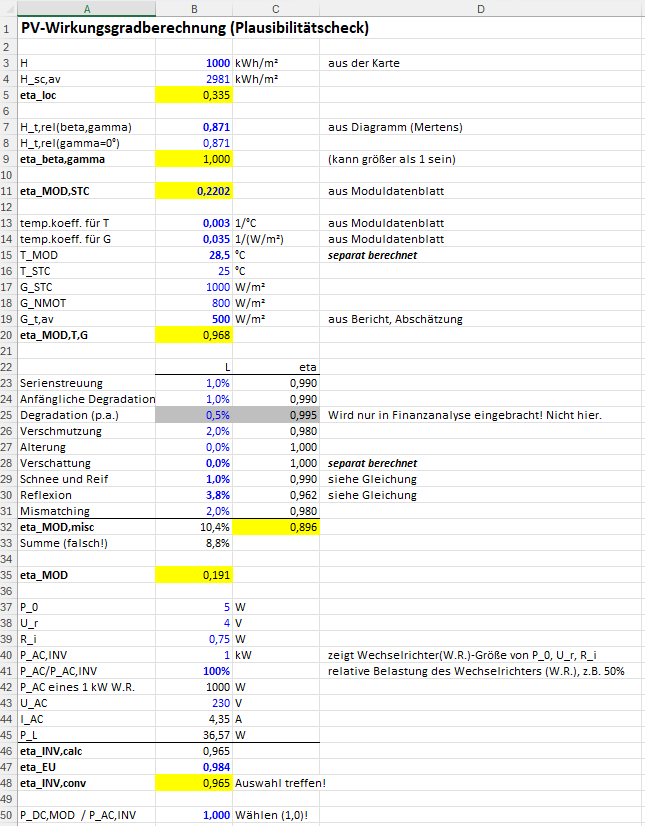
Wirkungsgrad Berechnung für PV-Anlagen als Plausibilitätscheck.
In das Bild klicken für eine vollständige Darstellung!
Ausgangspunkt der Überlegung zu den Wirkungsgraden der PV-Anlage war ein Diagramm mit der "Wirkungsgradkette der Photovoltaik". Nachdem die Parameter jetzt mit der Tabellenkalkulation abgeschätzt wurden, können die Werte in diese Bild eingezeichnet werden. Wirkungsgrade werden durch Multiplikation verknüpft. Mit dem Taschenrechner kann jetzt nachgerechnet werden, ob die Wirkungsgrade richtig zusammenpassen und welcher Verlust zwischen zwei beliebig gewählten Punkten in der Anlage auftreten.
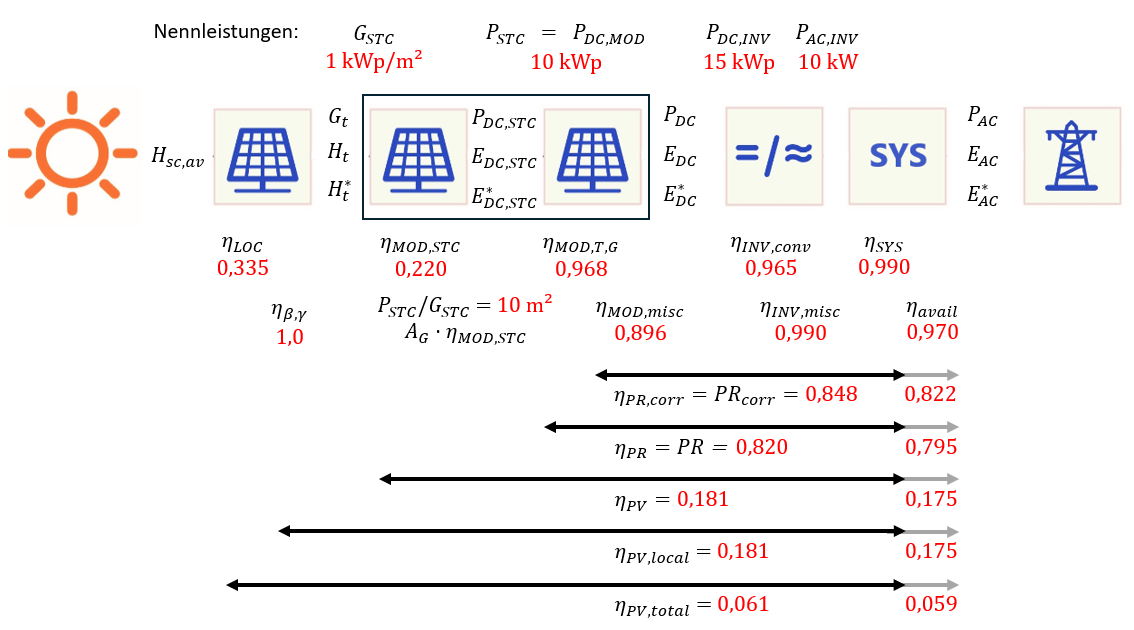
Wirkungsgradkette mit Beispieldaten.
Im Beispiel ergibt sich ein Anlagenwirkungsgrad (performance ratio), PR = 0,82. Das entspricht einem Verlust von 18 %.
Diese 18 % wurden hier mit einfachen Methoden ermittelt, was (geschätzt) mit einer Genauigkeit von ± 3 % erfolgt. Das ist zu mindestens ausreichend, um die Ergebnisse eines professionellen Tools auf Plausibilität zu kontrollieren.
Hohe Temperaturen könnten zwar zum dominierenden Verlust werden (bis zu 13 %, siehe oben), aber in Deutschland nur an wenigen sehr heißen Tagen um die Mittagszeit. Daher sind die Verluste zu ηMOD,T,G mit moderaten 3 % angegeben. Ein Vergleich der Teilwirkungsgrade zeigt ansonsten, dass die Zusatzverluste an den Solarmodulen (ηMOD,msic) dominieren. Dies liegt natürlich auch daran, dass die Verlustursachen inhaltlich allokiert wurden und viele Verluste den Solarmodulen zugeordnet wurden.
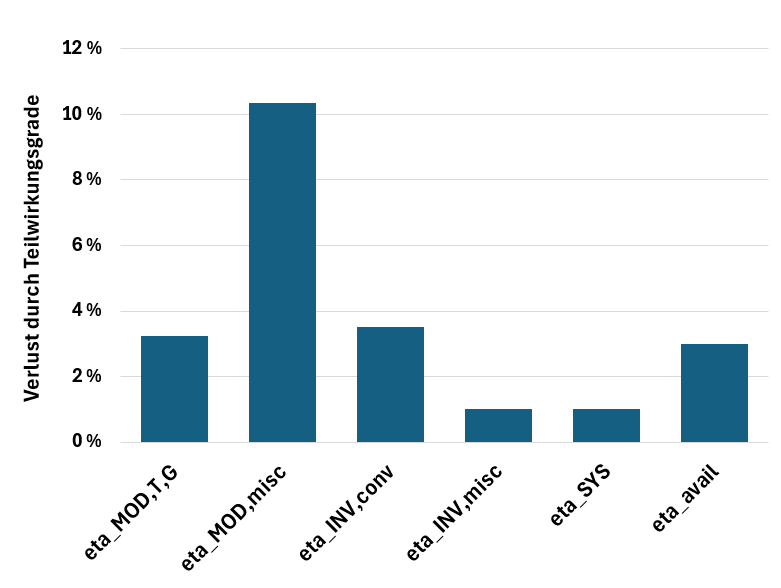
Separat betrachtet (daher hier nicht gezeigt) wird der: eta_MOD,STC Modulwirkungsgrad bei Standardtestbedingungen Ansonsten: eta_MOD,T,G Temperatur- und Globalstrahlungswirkungsgrad eta_MOD,misc Wirkungsgrad zur Berücksichtigung verschiedener Verluste an den Solarmodulen eta_INV,conv Wechselrichter-Umwandlungswirkungsgrad eta_INV,misc Wirkungsgrad zur Berücksichtigung verschiedener Verluste am Wechselrichter eta_SYS Wirkungsgrad zur Berücksichtigung verschiedener Verluste von Komponenten und Umständen im System eta_avail Wirkungsgrad = Verfügbarkeit des Systems |
Die Wirkungsgrade zur Berücksichtigung verschiedener Verluste an den Solarmodulen (miscellaneous module efficiencies), ηMOD,misc sind ebenfalls aufgeschlüsselt und graphisch dargestellt. Die Degradation (der Solarzellen) überwiegt. Hier dargestellt für ein mittleres Alter einer PV-Anlage (10 Jahre). Solar-Simulationsprogramme rechnen eine neue Anlage nur über ein Jahr. Diese Programme können bestenfalls die anfängliche Degradation berücksichtigen (im ersten Jahr). Finanzprogramme schließen die Degradation ein in die finanzielle Betrachtung über das Leben der Anlage (i.d.R. 20 Jahre). Verschattung ist mit 0 % angegeben, weil die Verschattung in Solar-Simulationsprogrammen in den Zeitschritten über den Tag und das Jahr berücksichtigt werden (statt pauschal). Wenn Verschattung vorhanden ist, dann kann dies die höchsten Verluste verursachen. Ansonsten ist die Reflexion am Glas der Solarmodule ein großer Verlust. Optimal ausgerichtete Module haben geringere Verluste durch Reflexion. Hier wurden horizontale Module angenommen (3,8 %). Selbst bei bester Ausrichtung machen die Verluste durch Reflexion aber immer noch 3 % aus.
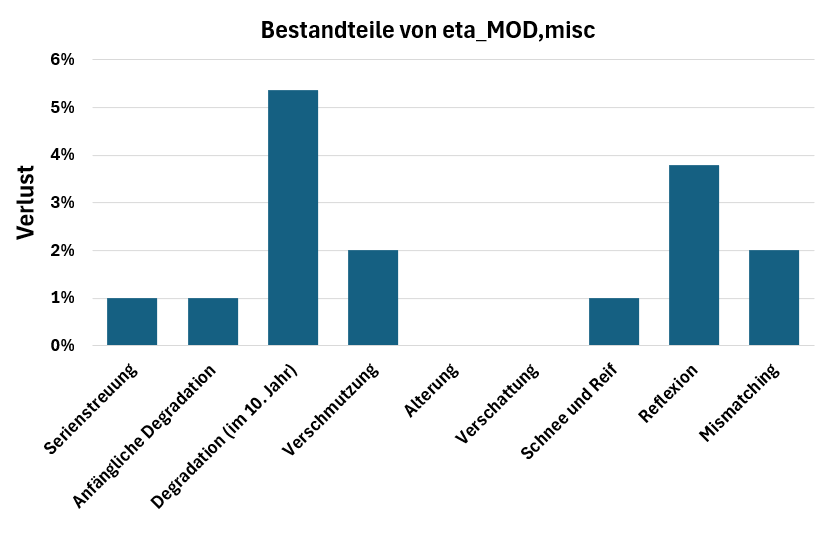 |
Mit den Wirkungsgraden können Parameter im System ineinander umgerechnet werden. Wichtig ist dabei der Anlagenwirkungsgrad (performance ratio), PR. Zusammen mit dem Modulwirkungsgrad bei Standardtestbedingungen werden die Strahlungsdaten am Eingang der PV-Anlage mit den Ausgangsdaten am Wechselrichter verknüpft. Wie oben bereits gezeigt, sind dies die drei Umrechnungen:
|
|
Diese und weitere Rechnungen sind im Umrechnungsschema dargestellt. Mit dem Umrechnungsschema werden viele Umrechnungen und Rechenwege übersichtlicher dargestellt als mit vielen einzelnen Gleichungen. Das Umrechnungsschema zeigt Parameter, Wert und Einheit in einem blauen Kasten. Die Umrechnung erfolgt mit den Umrechnungsfaktoren im grünen Kasten (grau unterlegt). Die Umrechnungsfaktoren stehen immer zwischen den Parametern, die jeweils ineinander umgerechnet werden sollen. Der Faktor ist dann richtig, wenn in der mit rotem Pfeil angezeigten Richtung umgerechnet werden soll. Soll in der entgegengesetzten Richtung gerechnet werden, so muss der Kehrwert des Parameters genutzt werden. In der oberen Zeile stehen die Leistungen (G, P). Darunter stehen die Energien (H, E). Beide sind durch zwei durchgezogene Linien voneinander getrennt, weil hier keine Umrechnung angeboten werden kann. Grund: Eine Umrechnung von Leistung in Energie für die PV-Anlage ist einfach nicht möglich, weil der Jahresverlauf, Monatsverlauf oder Tagesverlauf der Leistungen (ohne weiteres) nicht bekannt ist. Einfach möglich ist nur die Umrechnung über eine kurze Zeit mit (leidlich) konstanter Leistung (z.B. Δt = 6 Minuten): E = P·Δt . Übrigens, von einer Strahlungssumme (H, links) zu einer Energie (E, rechts) gibt es verschiedene Wege durch das Diagramm und damit unterschiedliche Faktoren, die multipliziert werden. Durch Kürzen im Produkt dieser Umrechnungsfaktoren kommt am Ende immer die gleiche Umrechnungsformel heraus.
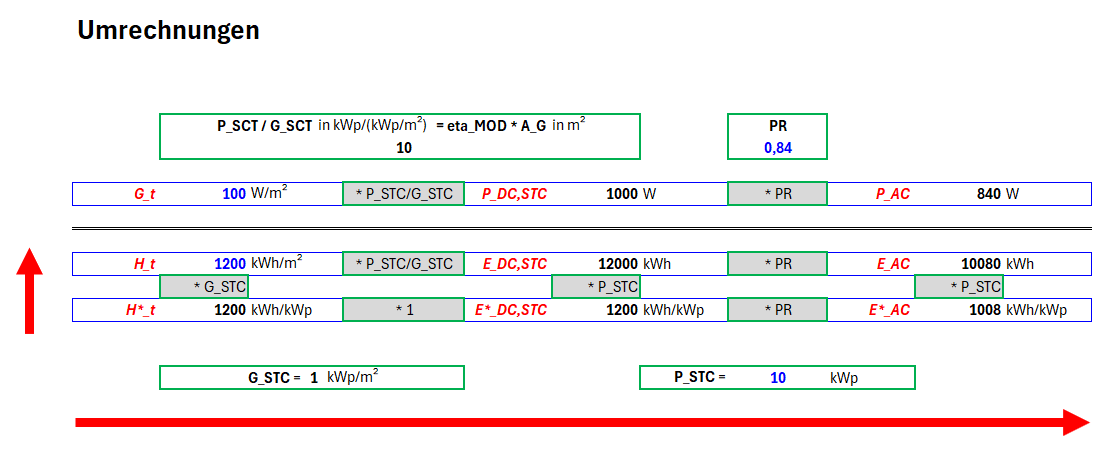
Umrechnung wichtiger Parameter von PV-Anlagen.

Umrechnung wichtiger Parameter von PV-Anlagen. Die Legende erkärt die Bedeutung der Zeichen.
Fläche der Module, AG
AG ist die Brutto-Kollektorfläche (gross collector area) des Moduls.
Das ist die grösste projizierte Fläche eines vollständigen Kollektors, ohne Vorrichtungen für die Befestigung.
Für eine bestimmte Nennleistung ist folgende Fläche erforderlich
|
Frage: Wie groß ist die Fläche einer 20 kWp-Anlage mit ηMOD = 20%? Antwort: 20 kW / 1 kW/m2 / 0,2 = 100 m2. |
Im Kopf teile ich die (Anzahl der) kWp durch den Wirkungsgrad und erhalte die Modulfläche in m2.
Erkenntnis: PV-Module werden nach kWp eingekauft. Der Preis richtet sich nach der Nennleistung (z.B. 1000 EUR/kWp). Der Wirkungsgrad ist daher (eher) egal, solange das Dach groß genug ist!
Nennleistung der PV-Anlage, PSTC (nominal power of the PV system)
Die PV-Anlage ist charakterisiert durch die Summe der Nennleistung der Module mit PSTC in
Kilowatt peak (kWp).
Das ist die Leistung unter
Standard-Testbedingungen (Standard Test Conditions, STC).
Das wurde bereits weiter oben beschrieben.
Die Nennleistung wird nur über sehr kurze Zeiten im Jahr erreicht, z.B.
mittags im Mai, wenn bei blauem Himmel mit einzelnen Wolken, die Wolken die Sonne freigeben und diese dann auf die kühlen Module scheint.

Nennleistungen von Anlagenkomponenten (Werte in rot).
Nennleistung des Wechselrichters am Ausgang, SAC,INV und PAC,INV (nominal AC power of the inverter)
Der Wechselrichter ist gekennenzeichnet durch seine Nennleistung am Ausgang als Scheinleistung, SAC,INV.
Dies ist die Leistungsangabe, die im Namen des Wechselrichters genannt wird und an erster Stelle im Datenblatt steht.
Am Ausgang wird Wechselstrom (alternating current, AC) bereitgestellt.
Die Nennleistung ist die maximal zulässige
Scheinleistung
des Wechselrichters. Die Scheinleistung, S = Ueff · Ieff
ergibt sich aus der Multiplikation der
Effektivwerte von
Spannung, U und Stromstärke, I.
Die Scheinleistung hat die Einheit Voltampere (VA oder kVA).
Gelegentlich wird auch kW angegeben, was strenggenommen die falsche Einheit ist.
Der Wert der Scheinleistung ist etwas größer als der Wert der Wirkleistung, P. die eingespeist und bezahlt wird.
Wenn der Wirkfaktor, cos φ = 0,9 beträgt, dann
muss die Nennleistung (Scheinleistung) des Wechselrichters um mindestens 1/0,9 = 11 % größer gewählt werden
als die Wirkleistung, die eingespeist werden soll.
Der Wechselrichter ist weiter gekennenzeichnet durch seine Nennleistung am Ausgang als Wirkleistung, PAC,INV. Wirkleistung, P ist die Leistung, die eingespeist und bezahlt wird. Es ist also die für die Praxis wichtigere Nennleistung. Die Nennleistung(!) als Wirkleistung wird per Definition mit cos φ = 0,9 berechnet. Möglich sind natürlich auch andere Wirkfaktoren (z.B. 0,95) und somit andere Wirkleistungen, die aber keine Nennleistung als Wirkleistung sind.
Phasenverschiebung und Wirkfaktor, cos φ (power factor)
φ ist die
Phasenverschiebung
zwischen Spannung und Stom. Es ist ein Winkel, der i.d.R. in Grad angegeben ist.
cos φ ist der
Wirkfaktor,
auch genannt Verschiebungsfaktor oder Power Factor, PF.
Im Fall der Netzeinspeisung folgt der Strom der Spannung. Die Phasenverschiebung ist dann per Definition ein positiver Wert.
Der Wirkfaktor, cos φ ist dimensionslos und ein Wert zwischen 0,9 und 1,0.
Die Norm VDE-AR-N 4105 (Erzeugungsanlagen am Niederspannungsnetz, Technische Mindestanforderungen) fordert, dass Photovoltaikanlagen in Deutschland in der Lage sein müssen, Blindleistung, Q (in var) bereitzustellen, um die lokale Netzspannung zu stabilisieren. Die Bereitstellung wird nicht bezahlt. Q = S · sin φ. Der Netzbetreiber fordert je nach Anlagengröße ein cos φ zwischen 0,9 und 0,95. Die Variation des Verschiebungsfaktors am Wechselrichter wird verwendet, um bereits vorhandene und unvermeidbar auftretende Blindleistungen im Stromnetz zu neutralisieren.
Nennleistung des Wechselrichters am Eingang, PDC,INV (nominal DC power of the inverter)
Ein Wechselrichter ist in der Lage eine erheblich höhere Leistung aufzunehmen, als es der Nennleistung am Ausgang entspricht.
Die maximal aufgenommene Leistung als Gleichstrom am Eingang des Wechselrichters, PDC,INV kann das 1,5-fache der Ausgangsleistung betragen.
Das schafft Flexibilität bei der Anlagenauslegung.
Aber natürlich wird die Leistung, die die AC-Nennleistung überschreitet abgeschnitten und ist damit verloren.
Das wurde oben
hier und
hier
unter Wirkleistungsbegrenzung besprochen.
Dimensionierungsfaktor, DF und andere Nennleistungsverhältnisse
Weiter oben wurde bereits das Verhältnis PDC,MOD / PAC,INV
zusammen mit der Wirkleistungsbegrenzung (clipping) angesprochen.
Dieses Verhältnis ist der Dimensionierungsfaktor, DF oder der Auslegungsfaktor (Sizing Ratio, SR).
Auch der Kehrwert des Dimensionierungsfaktors ist im Gespräch. Es ist das Wirkleistungsverhältnis, WV.
Weniger sinnvoll ist es, die Nennleistung der Module auf die DC-Nennleistung des Wechselrichters zu beziehen, weil Wechselrichter auf der Eingangsseite stark überdimensioniert sein können. Trotzdem ist es wichtig, Begriffe einordnen zu können, die in der Diskussion vorkommen. Der Überdimensionierungsfaktor (ÜDF) ist
.
Auch der Kehrwert des Überdimensionierungsfaktors ist im Gespräch. Es ist das Nennleistungsverhältnis (Nominal Power Ratio, NPR).
Energienutzungsfaktor
Der Energienutzungsfaktor, ENF ist das Verhältnis der ins Netz gespeisten Energie zum nutzbaren Energieangebot des PV-Generators,
EAC,INV / EDC,INV.
Der Wechselrichter-Umwandlungswirkungsgrad, ηINV,conv bleibt dabei unberücksichtigt (ηINV,conv = 1).
Es geht hier um Verluste aus einer möglichen Wirkleistungsbegrenzung (clipping).
Das wurde oben
hier und
hier besprochen.
Der Energienutzungsfaktor soll größer als 99 % sein. ENF kann aus den Verlusten (loss, L) durch Clipping errechnet werden.
Schieflast
Das Stromnetz ist ein
Dreiphasenwechselstromnetz (Drehstromnetz).
Unter
Schieflast, SL
versteht man die ungleichmäßige Belastung der
Außenleiter (Phasen) L1, L2 und L3 in einem Drehstromnetz.
Schieflast ist die größte Leistungsdifferenz (als Scheinleistung) zwischen den einzelnen Phasen.
Zu ermitteln ist also die größte Differenzen zwischen L1 und L2, L2 und L3 sowie L1 und L3.
Größere Schieflasten können ohne Kompensation im Extremfall wegen Überhitzung zu Schäden führen.
Die Einspeisung mit einem einphasigen Wechselrichter ist aus 4,6 kVA beschränkt
(VDE-AR-N 4105).
Mehrere einphasigen Wechselrichter müssen auf die Phasen verteilt werden.
Sinnvoll ist es, dreiphasige Wechselrichter zu verwenden.
Auch wenn dreiphasig eingespeist wird, darf die Differenz zwischen den einzelnen Phasen nie mehr als diese 4,6 kVA betragen.
CO2-Reduktion
Zu unterscheiden sind zwei Aspekte:
Zu 2.) Photovoltaikanlagen vermeiden Emissionen hauptsächlich aus Steinkohle (Anteil: 55 %), Erdgas (Anteil: 33 %) und Braunkohle (Anteil: 12 %) in Höhe von zusammen 0,746 kg/kWh CO2-Äquivalente."
In dieser Betrachtung entfallen 56 g/kWh auf die CO2-Äquivalente der Photovoltaik nach 1.), die damit nur 7,5 % der vermiedenen CO2-Äquivalente nach 2.) ausmachen. Der Nutzen der Photovoltaikanlagen entsteht aus der Differenz von 2.) 0,746 kg/kWh und 1.) 0,056 kg/kWh. Diese Differenz, der "Netto-Vermeidungsfaktor der Photovoltaik liegt bei 0,690 kg/kWh CO2-Äquivalente." (Quellen: Umweltbundesamt 2023a und Umweltbundesamt 2023b, archiviert).
PV-Planungssoftware arbeitet mit intern abgelegten Netto-Vermeidungsfaktoren. Auf diese Netto-Vermeidungsfaktoren kann mit dem Taschenrechner leicht zurück gerechnet werden. Die (konservativen) Annahmen sind beispielsweise in PV*SOL: 0,470 kg/kWh CO2-Äquivalente und in SUNNY DESIGN: 0,414 kg/kWh CO2-Äquivalente.
Mit dem Netto-Vermeidungsfaktor, mCO2,eq / EAC und der Anzahl der Jahre, nyear, über die ersparten CO2-Äquivalente aufsummiert werden, ergibt sich die gesamte Einsparung an CO2-Äquivalenten.
"Das Ergebnis für die versauernd wirkenden Luftschadstoffe fällt ... ebenfalls deutlich positiv aus. Nur im Bereich der Ozonvorläufersubstanzen und Staub ist die Bilanz negativ, hier wurden durch den Abbau benötigter Ressourcen und bedingt durch Produktionsprozesse zur Herstellung von PV-Modulen geringfügig mehr Emissionen verursacht als vermieden." (Umweltbundesamt 2023b)
Die Darstellung charakteristischer Parameter am Beispiel einer PV-Planungssoftware
Jede PV-Planungssoftware hat im Detail eigene Bezeichnungen für die Parameter der Photovoltaik.
Eine Zuordnung kann einfach gelingen, solange es bei der Namensgebung bleibt.
Es kann aber auch vorkommen, dass Parameter anders definiert werden. Dann wird eine Zuordnung schwieriger.
Was gemeint ist, wird gelegentlich erst deutlich, wenn den Abhängigkeiten der angegebenen Parameter mit dem Taschenrechner nachgegangen wird.
Am Beispiel einer Ergebnisdarstellung von SUNNY DESIGN werden die Angaben der PV-Planungssoftware den Variablennamen dieses Textes gegenübergestellt.

PV-Auslegungsdaten von SUNNY DESIGN erklärt und verglichen mit den Variablennamen in diesem Text.
In diesem Abschnitt geht es um Absorption, Reflexion, Transmission und Extinktion. Unter "Grundlagen" wurden die Begriffe schon genannt im Zusammenhang mit der Globalstrahlung. Hier geht es um eine etwas formalere Darstellung aus der Physik und die Anwendung im Gebiet "Physik der Atmosphäre" und letztlich auch wieder um die Anwendung in der Photovoltaik. Weitere Begriffe werden eingeführt: Air Mass und Optische Dicke.
Absorption, Reflexion und Transmission
Strahlung durch die Atmosphäre wird teilweise verschluckt (absorbiert) oder gestreut (diffus reflektiert).
Der Rest der Strahlung wird durchgelassen durch die Atmosphäre. Es geht also um
Absorption (absorbance) diffuse Reflexion oder Streuung (diffuse reflection, scatter, remission), und Transmission (transmittance).
Es geht um die Leistung der Strahlung, P (in W) oder um die Leistung der Strahlung, P" (in W/m2), die aufgeteilt werden.
Daher machen Absorption, diffuse Reflexion und Transmission jeweils nur einen Anteil der Gesamtleistung der Strahlung, P0 bzw. P"0 aus.
Die Anteile haben folgende Bezeichnungen:
Transmissionsgrad (transmittance), T,
Absorptionsgrad (absorption), A,
Reflexionsgrad (remission), R.
Alle Anteile zusammen ergeben eins. Es gibt nichts anderes als Transmission, Absorption und diffuse Reflexion.
Nach dem Gesetz von Lambert-Beer:
Gelegentlich werden Absorption und diffuse Reflexion zusammengefasst. Beide Vorgänge zusammen werden Extinktion, Auslöschung oder Dissipation genannt (extinction). Der Anteil an der Gesamtleistung der Strahlung, P0 ist
und hat die Bezeichnung Dissipationsgrad (extinction), E.
Optische Dicke und Extinktionskoeffizient
Die optische Dicke wird auch optische Tiefe (optical depth) genannt.
Hier jetzt zur optischen Dicke nach der Definition in der Physik. Zur optischen Dicke nach der Definition im Zusammenhang mit der Solarstrahlung siehe unten.
Die optische Dicke eines Materials hängt ab von den Frequenzen des Lichtes oder der Art des Spektrums. Sie errechnet sich durch Integration des Absorptionskoeffizienten, a über den Lichtweg, l.
In einem homogen Medium vereinfacht sich die Integration zur Multiplikation.
Der Absorptionskoeffizient (attenuation coefficient) – besser: Extinktionskoeffizient (extinction coefficient), a. Die Bezeichnung Extinktionskoeffizient (extinction coefficient) wird häufig in der Meteorologie und Klimatologie verwendet.
Die Dimension des Absorptionskoeffizienten, a ist 1/Länge, also 1/m. Ein großer Absorptionskoeffizient bedeutet, dass das Material die betrachtete Strahlung relativ stark abschirmt, ein kleiner dagegen, dass es durchlässiger für die Strahlung ist. Die Größe misst den exponentiellen Abfall der Intensität. Ein Koeffizient von 1 1/m bedeutet, dass von der Strahlung nach Durchquerung von 1 m noch 36,8 % übrig bleiben (T = e-1 = 0,368). Ein anderes Vorgehen verwenden statt e die Basis 10 und damit den dekadische Absorptionskoeffizient.
In der Bezeichnung Absorptionskoeffizient ist der Begriff Absorption nicht im engeren Sinn der Abgabe von Strahlungsenergie an das Medium zu verstehen. Zur hier gemeinten Intensitätsabnahme tragen vielmehr auch Streuprozesse bei, die die Strahlung nur aus ihrer Richtung ablenken. Daher ist die Bezeichnung Extinktionskoeffizient (extinction coefficient) korrekter.
Es gibt zwei Möglichkeiten die Konzentration, C zu berechnen.
Darin ist pi der Partialdruck des betreffenden Stoffes und kB = 1,380649·10-23 J/K die Boltzmann-Konstante.
σ ist der Wirkungsquerschnitt.
Entsprechende Parameter sind vollständig nicht verfügbar. Daher ist eine Berechnung aus der Theorie heraus wie hier beschrieben allein nicht möglich.
Jetzt zur Praxis und zur üblichen Schreibweise in der Photovoltaik und in der Physik der Atmosphäre. Hier wird der Transmissionsgrad (transmittance) geschrieben als
.
Daraus ergibt sich eine etwas andere Definition von τ. Es ist jetzt τPV = τphysics / m. Im Zusammenhang mit der Solarstrahlung ist τ also anders definiert als allgemein in der Physik. Die relative Länge des Weges durch die Atmosphäre, m wird abgespalten.
Optische Luftmasse (Air Mass) und optische Dicke der Atmosphäre
In der Gleichung (oben) ist m die optische Luftmasse (optical air mass, AM) – oft auch nur kurz Luftmasse (air mass) genannt.
AM ist ein Maß für die Weglänge durch die Atmosphäre bis zum Meeresniveau, die von den Lichtstrahlen der Sonne durchquert wird,
bezogen auf die Weglänge der Vertikalen.
Die optische Luftmasse variiert mit dem Sonnenzenitwinkel, θz und dem lokalen Luftdruck, p,
der sich mit der Höhe über Meeresniveau der PV-Anlage ändert.
p0 ist der normale atmosphärische Druck in Meereshöhe (1013 hPa).
Der Luftdruck, p wird gemäß der Internationale Standardatmosphäre nach der
Höhenformel
berechnet. Siehe auch
Scholz (2012, S.5-7, PDF).
Die Höhenformel für die Troposphäre ist gültig bis in 11 km Höhe und damit ausreichend auch für PV-Anlagen in den Bergen.
,
mit ka = 2,2558·10-5 1/m = 0,02558 1/km. H: Geopotentielle Höhe. H ≈ h . h: Geometrische Höhe.
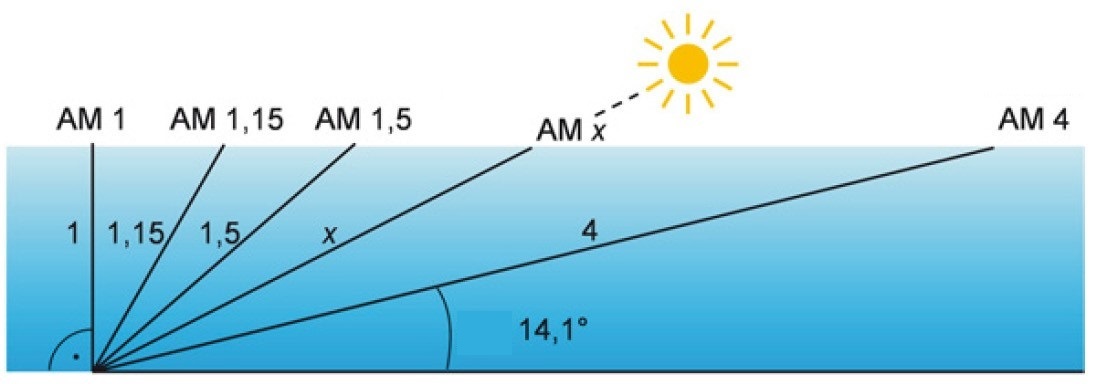
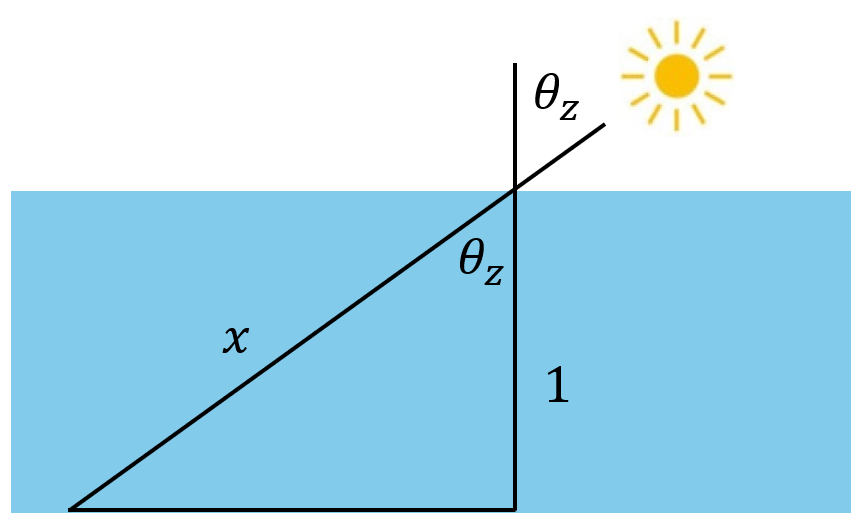
Erklärung des Begriffes Air Mass (AM). Die Zahl x = 1 / cos θz gibt die Wegverläng gegenüber dem senkrechten Durchtritt durch die Atmosphäre an.
Hier für p = p0.
Links: Quelle: K. Mertens, www.lehrbuch-photovoltaik.de, Bild 2.3.
Die optische Dicke der Atmosphäre (optical depth of the atmosphere, OD) – definiert über die optische Masse – setzt sich zusammen aus
Durch den Klimawandel kommt es zu mehr Sonnenscheinstunden. Im Jahr 2022 wurden in Niedersachsen 1940 Sonnenscheinstunden gemessen. Dies im Vergleich zu 1456 Sonnenscheinstunden in der Referenzperiode 1961-1990. Die Jahresmitteltemperatur in Niedersachsen erreichte dadurch 2022 ungewöhnliche 10,7 °C (gegenüber 8,6 °C in der Referenzperiode 1961-1990) (Quelle: DWD). Im Jahr 2022 wurde in Deutschland eine mittlere Jahressumme der Globalstrahlung von 1227 kWh/m2 erreicht. Das ist der höchste Wert seit Beginn der Aufzeichnungen im Jahr 1983. Seit 1983 ist die Jahressumme der Globalstrahlung in Deutschland im Mittel um 3,6 kWh/m2 pro Jahr gestiegen. Das ist (bezogen auf den Wert von 2022) ein Anstieg der Jahressumme von 0,29 % pro Jahr (Quelle: DWD). Die Degradation der PV-Module wird i.d.R. mit 0,5 % pro Jahr angesetzt. Der Klimawandel kann die Degradation also etwa zur Hälfte ausgleichen. Viel mehr Daten gibt es auf der Homepage zur Strahlungsklimatologie beim DWD.
Müller (2018) ermittelt in seiner Dissertation "Unsicherheiten von Ertragsprognosen für Photovoltaik-Kraftwerke unter besonderer Berücksichtigung langfristiger Variationen des Solarstrahlungs-Potenzials" eine "Brightening"-Phase mit zunehmender Solarstrahlung seit am Anfang der 1980er Jahre. Aufgrund dieser Trends kommt es im Mittel zu Abweichungen in Höhe von etwa 3 % zwischen der horizontalen Globalstrahlung in einem Referenzzeitraum und der Globalstrahlung in einem darauf folgenden 20jährigen Prognosezeitraum. Für die Einstrahlung in geneigte Flächen sind noch deutlichere Abweichungen zu erwarten. Auf Basis der Untersuchungen wird zur Reduzierung des Einflusses von Strahlungstrends vorgeschlagen, anstatt der bisher als Standard anzusehenden Verwendung möglichst langfristiger Referenzzeiträume, lediglich 10jährige Referenzzeiträume zur Bestimmung des Solarstrahlungs-Potenzials zu verwenden. Schließlich werden bereits erstellte Ertragsprognosen mit Messungen an kommerziell betriebenen PV-Anlagen verglichen. Der Vergleich zeigt, dass Ertragsprognosen, die sehr langfristige Referenzzeiträume verwenden, die gemessenen Erträge systematisch um etwa 5 % unterschätzen.
Eine höhere Jahressumme der Globalstrahlung steigert den Energieertrag einer PV-Anlage. Das ist aber nur ein Faktor von mehreren. Eine steigende Temperatur vermindert den Ertrag. Eine steigende Windgeschwindigkeit wirkt kühlend auf die Module und damit indirekt steigernd auf den Ertrag. Alles zusammen genommen prognostiziert Jerez (2015) eine Abnahme des PV-Ertrages in Deutschland bis 2080 um 2 % bis 5 % im Mittel der verschiedenen Szenarien.
Jerez, S., et al., 2015. The impact of climate change on photovoltaic power generation in Europe. In: Nature Communications, Vol. 6, Art. 10014. https://doi.org/10.1038/ncomms10014.
A) Anlagen mit Volleinspeisung:
Dem Anlagenkennfeld (s.o) oder GSA kann der optimale Neigungswinkel für feste Installation (optimum inclination, optimum angle, OPTA), βopt entnommen werden.
Als "optimal" wird dabei der Neigungswinkel angesehen, der über das Jahr den höchsten Ertrag bringt.
Dies ist auch wirtschaftlich korrekt bei Anlagen mit Volleinspeisung.
Im Anlagenkennfeld ist der optimale Neigungswinkel der bei Ht,rel = 100 %.
100 % tritt (auf der Nordhalbkugel) auf bei einem Azimut von 0° (Süden).
Genaugenommen ist der optimale Azimut, γopt um 5° bis 10° in Richtung Osten verschoben. Der Wert des optimalen Azimuts ist dann etwa 7,5° bzw. 172,5° (je nach Definition). Das liegt an den geringeren Temperaturen am Morgen und damit einer höheren Leistung bei kälteren Modulen. Deutlich wird das nur in einer detaillierteren Simulation, die auch die Temperatur im Modul berücksichtig. Eine morgens geringere Umgebungstemperatur und eine statische Berechnung der Modultemperatur führt bereits zu einer Verschiebung. Deutlicher wird dieser Effekt, wenn die Temperatur in den Modulen dynamisch gerechnet wird. Die Module müssen sich erst aufheizen. Hohe Modultemperaturen sind damit in den Nachmittag verschoben. Eine optimale PV-Auslegung wird immer den Zustand bevorzugen, bei dem die Bedingungen zu einer hohen Ausbeute führen. Siehe dazu Burger (2005, Bild 10 und 11), Quellenangabe oben.
Aus dem Anlagenkennfeld kann man optimale Neigungswinkel auch für andere Ausrichtungen ablesen: Für Ausrichtungen zwischen Westen über Norden nach Osten ist der optimale Neigungswinkel 0°. Je weiter der Azimut (bei Südausrichtungen) von Süden abweicht, desto flacher ist der optimale Winkel. Kann eine Ausrichtung nach Süden ermöglicht werden, dann ist nach Mertens/PV*SOL βopt = 35° (Hamburg, Berlin, München). Nach GSA ist für Deutschland OPTA zwischen 32° und 40° (Hamburg, Berlin, München: 37°).
B) Anlagen mit Eigenverbrauch und Überschusseinspeisung:
Eigenverbrauch geht vor Überschusseinspeisung aufgrund der Stromtarife.
Das hat Auswirkungen auf die optimale Ausrichtung der Module.
1.) Falls der Verbrauch nahezu konstant sein sollte,
so müssen die Module so ausgerichtet sein, dass die PV-Leistung
a) in den leistungsschwachen Stunden am Morgen und am Abend und
b) in den leistungsschwachen Monaten im Winter angehoben wird.
Das gilt aber nur, wenn die Anlage so groß ist, dass am Mittag und im Sommer mehr PV-Leistung bereit steht als gebraucht wird.
a) erfordert dann eine Ausrichtung nach Osten und Westen, b) erfordert einen größeren Neigungswinkel und Südausrichtung.
2.) Falls ein höherer Verbrauch (wie im Haushalt) morgens und nachmittags auftritt, so ist wieder eine Ausrichtung nach Osten und Westen vorteilhaft.
Neben der Geometrie zur Sonne gibt es weitere Argumente für eine Ost-West-Ausrichtung bei Eigenverbrauch und Überschusseinspeisung.
1.) Bei einem Flachdach gilt:
Sollte die Dachfläche begrenzt sein, so können mehr Module untergebracht werden ohne Eigenverschattung.
Die Ost-West-Ausrichtung bietet eine einfache Unterkonstruktion, ist wenig Windanfällig und
ermöglicht trotzdem einen Neigungswinkel, mit dem
a) bei Regen eine Selbstreinigung der Module erzielt wird und
b) der Schnee eher von den Modulen abrutschen kann als bei horizontaler Anordnung der Module auf dem Flachdach.
Die PV-Leistung hat weniger ausgeprägte Spitzen (mittags). Das hat zwei Effekte:
a) Dadurch kann der Wechselrichter leicht unterdimensioniert werden. Dies spart bei den Anschaffungskosten des Wechselrichters.
Stringwechselrichter eignen sich für Ost-West-Anlagen,
da sie zwei oder mehrere MPP-Tracker (Maximum Power Point Tracker) haben. Ost- und Westmodule bilden dann unterschiedliche Strings.
b) Ein Batteriespeicher könnte diese Spitzen für den Eigenverbrauch nutzbar machen, kostet aber.
Durch die Ost-West-Ausrichtung kann der Batteriespeicher kleiner gewählt werden (oder obsolet werden).
Statt in die (teure) Batterie kann evtl. wirtschaftlicher in mehr Modulfläche investiert werden.
Dies kann den geringeren Ertrag der Ost-West-Ausrichtung ausgleichen.
2.) Bei einem Satteldach in Ost-West-Ausrichtung gilt:
Durch den Eigenverbrauch hält sich der Nachteil dieser Dachanordnung in Grenzen (ist nicht so gravierend wie bei der Volleinspeisung).
Die Neigung des Daches soll aber nicht zu steil sein, ansonsten ist
der Gesamtertrag zu gering und es kann der erforderliche Eigenverbrauch mittags nicht gedeckt werden.
Diese Überlegungen sind nur qualitativ. Benötigt werden konkrete Zahlen aus einem Solar-Simulationsprogramm (s.u.). Wichtig ist, dass das Simulationsprogramm mit einem passenden, realistischen Lastgang des Verbrauchers arbeitet. Es müssen viele verschiedene Varianten des Anlagekonzeptes durchgerechnet und systematisch verglichen werden.
Im Abschnitt Strahlungssumme, H mit Klimaeinflüssen wurde gezeigt, dass es wichtig ist, die Jahres- oder Monatssummen bei Berücksichtigung des Klimas des Standortes zu kennen. Die Globalstrahlung an einem wolkenlosen Tag (s.o.) kann man nach den Gesetzen der Physik berechnen. Wettereinflüsse (Wolken) müssen durch eine Klimastatistik berücksichtigt werden.
Die klassische Handbuchmethode ist in Duffie (1980) in Abschnitt 2.7 beschrieben und zeigt, wie man die Monatssummen, Hm ermitteln kann.
Die Jahres- oder Monatssummen mit Wettereinfluss werden dabei nicht ausgehend von der Globalstrahlung an einem wolkenlosen Tag, Gc berechnet (s.o.) – wie man annehmen könnte. Das liegt daran, dass der "wolkenlose Tag" nicht eindeutig definiert werden kann. Stattdessed wird ausgegangen von der Tagessumme, H0d der extraterrestrischen Sonnenstrahlung (Duffie 1980, Gl. 1.8.3) eines mittleren Tages im Monat. ndm ist die Anzahl der Tage im jeweiligen Monat (days per month).
Der Standort wird einem Klimatyp und einem Vegetationstyp zugeordnet (Norddeutschland: Mittelwarmes Waldklima, konstant feucht, Regen über das Jahr verteilt; Laubwald). Für den Klimatyp von Hamburg (Norddeutschland) ist a = 0,22 und b = 0,57. Die Parameter a und b sollten auch für andere vergleichbare Klimazonen gelten. Für andere Klimatypen siehe Duffie (1980, Tabelle 2.7.2). Als weiter Parameter geht die relative Sonnenscheindauer n/N in die Rechnung ein. n sind die Sonnenscheinstunden pro Tag, N sind die Tageslichtstunden von Sonnenauf- bis untergang (Duffie 1980, Gl. 1.6.8 mit 1.6.1 abhängig von geographischer Breite, ϕ und Deklination, δ). Die Sonnenscheinstunden in Deutschland je Monat sind für 1099 Stationen in dieser Excel-Tabelle (Download) angegeben (Quelle: DWD). Die Sonnenscheinstunden anderer Orte sind auf Wikipedia zusammengetragen worden.
Alternativ kann die relative Sonnenscheindauer aus Karten vom "The European Database of Daylight and Solar Radiation" S@tel-Light (Anmeldung erforderlich) bezogen werden (weniger genau): Hier die Karten für Deutschland mit der relative Sonnenscheindauer im Jan, Feb, Mrz, Apr, Mai, Jun, Jul, Aug, Sep, Okt, Nov, Dez und All Year als Jahresmittelwert. Für Hamburg ergeben sich nach S@tel-Light geringere Werte der relative Sonnenscheindauer als nach DWD.
Dies sind dann die Eingabedaten und Ergebnisse für Flensburg (ϕ = 55°) mit den DWD-Daten zu den Sonnenscheinstunden:
Monat Jan Feb Mrz Apr Mai Jun Jul Aug Sep Okt Nov Dez Tage im Monat, n_dm 31 28 31 30 31 30 31 31 30 31 30 31 H_0d in kWh/m², φ = 55° 1,70 3,13 5,48 8,19 10,39 11,40 10,90 9,00 6,40 3,80 2,01 1,34 Jahressumme, H_0: 2249 kWh/m² % Sonnenschein, n/N 17% 23% 30% 42% 47% 42% 44% 46% 38% 31% 21% 16% Durchschnitt : 33% Monatssumme, H_m in kWh/m² 16,6 30,5 66,3 113,3 158,1 157,7 158,6 133,9 83,7 46,8 20,6 12,9 Jahressumme, H : 999 kWh/m² |
In der Praxis nutzt man – wie wir oben gesehen haben – die Daten aus dem Global Solar Atlas (GSA). Hier das Beispiel Flensburg (Detailansicht). Der Atlas zeigt (in grün) eine Strahlungssumme auf einer horizontalen Fläche, H von 994 kWh/m2 (pro Jahr). Das passt zum berechneten Wert aus der Tabelle.
In der Einleitung wurde das Planen von PV-Anlagen unterteilt in:
Zu 2. gibt es die Solar-Simulationsprogramme, die nach der Methode der Zeitschritt-Simulation arbeiten und einen jährlichen Energieertrag, EAC der Solaranlage berechnen. Die Globalstrahlung wird den Programmen in stündlicher Auflösung geliefert. Jeder Stundenwert wird in 60 Minutenwerte zerlegt. Minutenwerte der in der Berechnung sind vor allem wichtig, um Ertragseinbußen durch Wechselrichter-Unterdimensionierung, Wechselrichter-Abregelung oder das Zusammenspiel von PV-Anlage, Verbraucher und Speichern möglichst realistisch zu simulieren.
Zu 3. gibt es entweder spezialisierte Programme, oder es wird die finanzielle Bewertung in die Solar-Simulationsprogramme integriert.
Es gibt Online-Datenbanken (Global Solar Atlas, PVGIS, ...), die ihren Schwerpunkt darin haben, Globalstrahlung, H auf eine horizontale Fläche, Globalstrahlung, Ht auf die geneigte Fläche und die Wetterdaten zu liefern. Es werden Jahres- und Monatssummen ausgegeben. Auch Daten in feinerer Auflösung werden teilweise zum Download angeboten. Diese Online-Datenbanken berücksichtigen die Parameter der PV-Anlage nur grob in Form von einer Reihe abgeschätzter Einzelverluste.
Die Solar-Simulationsprogramme kombinieren hochaufgelöste Strahlungs- und Wetterdaten mit den Anlagenzuständen (Modultemperatur, Wirkungsgrade der Komponenten, ...) sowie mit dem Stromverbrauch eines Nutzers, um daraus einen Jahresertrag, EAC zu berechnen. Eine typische PV-Planungssoftware (PV*SOL, SUNNY DESIGN, ...) führt eine Solar-Simulation durch und unterstützt bei der Detailauslegung (Stringverschaltung) sowie bei der finanziellen Bewertung. Solar-Simulationsprogramme können Sachverhalte genauer berechnen als es mit einfachen Gleichungen, Tabellen oder Diagrammen möglich ist. Sie haben ihren Schwerpunkt in der genauen Darstellung der PV-Anlage.
Solar-Finanzprogramme nutzen die Ergebnisse der Online-Datenbanken als Eingabe und berechnen darauf aufbauend die weiteren finanziellen Ergebnisse in Jahresschritten über das Leben der Anlage (oft 20 Jahre).

World Bank: Global Solar Atlas (GSA) 
https://globalsolaratlas.info
Methodology
Berechnet alles von Strahlungsdaten bis zum Jährlichen Energie-Ertrag (annual photovoltaic energy output), EAC und Spezifischem Energieertrag (specific photovoltaic power output), eAC in kWh/kWp.
Das Tool sollte zur Überprüfung des Spezifischen Energieertrags, eAC in kWh/kWp aus SUNNY DESIGN genutzt werden.
Photovoltaic Geographical Information System (PVGIS) 
https://re.jrc.ec.europa.eu/pvgis
PVGIS User Manual
PVGIS provides information for any location in the world, except the North and South Poles: Photovoltaic Performance, Solar Radiation, Typical Meteorological Year. Sehr gut, wurde aber evt. von GSA überholt.
National Renewable Energy Laboratory (NREL): PVWatts Calculator 
https://pvwatts.nrel.gov/pvwatts.php
PVWatts Manual, 2014 mit Gleichungen! (Archiv)
Easy to use. Estimates the energy production of grid-connected photovoltaic (PV) energy systems throughout the world.
Performance data and Typical Meteorological Year (TMY) hourly weather data from NSRDB!
National Renewable Energy Laboratory (NREL): National Solar Radiation Database (NSRDB)
https://nsrdb.nrel.gov/data-sets/tmy Typical Meteorological Year (TMY) Data (via PVWatts)
National Solar Radiation Database
Europe, Africa & Asia: Weather Data 2017, 2018, 2019, 15-min-interval: Temperature, Clearsky DHI, Clearsky DNI, Clearsky GHI, Cloud Type, Dew Point, DHI, DNI, GHI, Ozone, Relative Humidity, Solar Zenith Angle, Surface Albedo, Pressure, Precipitable Water, Wind Direction, Wind Speed,
Cloud Types: 'Clear': 0, 'Probably Clear': 1, 'Fog': 2, 'Water': 3, 'Super-Cooled Water': 4, 'Mixed': 5, 'Opaque Ice': 6, 'Cirrus': 7, 'Overlapping': 8, 'Overshooting': 9, 'Unknown': 10, 'Dust': 11, 'Smoke': 12
Umweltinstitut München e.V. 
https://umweltinstitut.org/energie-und-klima/mitmachaktionen/wirtschaftlichkeit-von-solaranlagen/berechnungstabellen-fuer-solaranlagen
Berechnet detailliert den wirtschaftlichen Vorteil einer Photovoltaik- oder Solarthermie-Anlage. Excel-Download.
Valentin Software GmbH: PV*SOL Online
https://pvsol-online.valentin-software.com
Photovoltaik-Rechner zur Simulation und Ertragsberechnung von Photovoltaik-Anlagen.
Hilfreich das Handbuch zum Programm (PDF): Valentin Software, 2013: PV*SOL advanced. 4 Basis of Calculation (S. 19), 17 Glossary (S. 152)
Leondo media UG: Solarrechner für PV-Anlagen
https://www.pv-berechnung.de/rechner
"Leistungsstarker Online-Solarrechner berechnet Ertrag, Wirtschaftlichkeit, Rentabilität, Auswirkungen von Verschattungen, Bilanzierung mehrerer Solarflächen, mit oder ohne Speicher, stundengenaue Berechnung von Ertrag und Verbrauch, berücksichtigt individuellen Stromverbrauch.
Gespeicherte Projekte können über einen angegebenen Link erneut aufgerufen werden. Im PV Rechner gemachten Angaben werden automatisch nach 90 Tage gelöscht.
Fronius International GmbH: Solar.creator
https://creator.fronius.com
"Dimensionieren Sie Ihre Photovoltaik-Anlage mit den aktuellsten Modulen und allen verfügbaren Fronius Wechselrichtern." Daher evtl. etwas eingeschränkt.
Stiftung Warentest: Photovoltaik Rechner
https://www.test.de/Photovoltaik-Rechner-1391893-0
Rendite für Anlagen mit einer Spitzenleistung bis zu 30 kWp. Eigenverbrauch mit Überschusseinspeisung oder Volleinspeisung. Mit Speicher oder ohne.
IBC SOLAR AG
https://stromrechner.ibc-solar.de
IBC Solarstromrechner errechnet die Stromkostenersparnis durch Eigenverbrauch – mit oder ohne Speicher. Einfache Dachbelegung mit Modulen. Einfaches Tool.
DGS: pv@now easy / pv@now easy Ü20 / PV-Stromkostenrechner
https://www.pv-now-easy.de (PV-Anlage, Speicher, Wärmepumpe und Elektro-Fahrzeug)
DGS wirbt mit: "Rechentool mit nur vier Eingabegrößen".
https://www.pv-now-easy-ue20.de (Weiterbetriebsoptionen für Ü20-PV-Anlagen)
https://www.dgs-franken.de/service/pv-stromkostenrechner (Was kostet die Kilowattstunde Solarstrom?)
ARGE NFSim (Unternehmensberatung), Österreich: PV-Rechner
https://www.nfsim.eu/pv-simulator
Die Ertragsdaten basieren auf PVGIS unter der Annahme optimaler (unverschatteter) Bedingungen. Die wirtschaftliche Betrachtung basiert auf typischen (FESTEN!) Kosten. Angaben basieren auf durchschnittlichen Werten nur zur Vorinformation.
SENEC GmbH: Solarrechner
https://solarrechner.senec.com
Liefert wenige Daten für einfache PV-Anlagen. Ansonsten: Kontaktformular.
Eugen Wagner: Photovoltaik Rechner
https://www.rechnerphotovoltaik.de
Berechnet einen "groben Richtwert" der Energiemenge und Wirtschaftlichkeit.
Prof. Quaschning: Diverse kleine Solar-Tools
https://www.volker-quaschning.de/software
https://solar.htw-berlin.de/rechner
Prof. te Heesen: Energietools
https://www.umwelt-campus.de/energietools
BayWa AG: Solar-Planit
https://solar-distribution.baywa-re.lu/de/services/kostenloses-auslegungstool-solar-planit
Kostenlos, aber Registrierung erforderlich. Eigenaussagen: Planung kompletter PV-Anlagen: Montagesystem, Module, Wechselrichter, Batteriespeichersystem. Statik berechnen und eine transparente Ertragsprognose erstellen. Photovoltaik-Anlage dem Kunden präsentieren als PDF.
SolarEdge: PV-Anlagendesigner
https://www.solaredge.com/de/produkte/software-tools/designer
Sehr umfangreich. Eigenaussagen: "Es sind keine Lizenz- oder Abonnementgebühren erforderlich. Beinhaltet kostenlose, automatische Upgrades."
National Renewable Energy Laboratory (NREL), USA: System Advisor Model (SAM)
https://sam.nrel.gov
Sehr umfangreich. Profi-Tool. Eigenaussagen: "Free desktop application. To investigate technical, economic, and financial feasibility of renewable energy projects. PV systems, from small residential rooftop to large utility-scale systems."
Regierung von Kanada: RETScreen
https://natural-resources.canada.ca/maps-tools-and-publications/tools/modelling-tools/retscreen/7465
https://de.wikipedia.org/wiki/RETScreen
Viel mehr als PV. Freie Version kann weder speichern noch drucken.
Concordia University, Montreal, Canada: INSEL 8
https://insel.eu
Das Programm hat eine lange wechselvolle Geschichte. Blockdiagramm Simulationssystem – erfordert i.d.R. lange Einarbeitung! Programmierung von Anwendungen aus dem gesamten Bereich der Erneuerbaren Energietechnologien u.a. Photovoltaiksysteme.
Deutsches Zentrum für Luft- und Raumfahrt (DLR), Institut für Solarforschung: greenius - The Green Energy System Analysis Tool
greenius
"Der Fokus der Software liegt zwar im Bereich solarthermischer Kraftwerke, doch stehen seit langem auch Modelle für die detaillierte Simulation von weiteren erneuerbaren Technologien zur Verfügung. Dazu gehören nicht-konzentrierende Solarkollektoren zur Prozesswärmebereitstellung, Photovoltaik-Anlangen und Windkraftparks."
Solar Campus, Schweiz: Solar-Toolbox
http://www.solar-toolbox.ch
Solar-Toolbox requires Adobe Flash.
DGS: pv@now
https://www.pv-now.de (Online-Programm zur Wirtschaftlichkeit von Photovoltaikanlagen)
DGS-Franken wirbt mit: "Bewertung der Wirtschaftlichkeit von Photovoltaikanlagen in allen denkbaren Betreibermodellen."
PVsyst SA, Switzerland: PVsyst
https://www.pvsyst.com
Ursprünglich von der Universität Genf. Sehr umfangreich. Informatives Hilfe-System.
Luxea GmbH: SOLinvest
https://www.luxea.de/solinvest/
Beispiel: Ergebnisdarstellung mit SOLinvest, 2013
Hottgenroth Software AG: PV-Start & PV-Planer
Paket 1 und Paket 2
PV-Planer Vollversion
TRIENERGY Schweiz AG: PV Simulation Software TRI-DESIGN
https://www.tritec-energy.com/software
Für Kunden des TRI-STAND Montagesystems kostenlos.
SOLARSCHMIEDE Software GmbH (Vertrieb): SENEC.Simulation
https://www.solarschmiede.de/online-shop/software/senec-simulation
Photovoltaik-Planungssoftware von SENEC GmbH.
SOLARSCHMIEDE Software GmbH (Vertrieb): PVscout
https://www.solarschmiede.de/online-shop/software/pvscout-2-0-premium
Herstellerunabhängige Auslegungssoftware
Ninox Software GmbH: Ninox ‐ "Die ultimative Software für Photovoltaik-Profis"
https://ninox.com/de-low-code-loesung/photovoltaik
Entwickelt für Solarteure. Preis auf Anfrage.
HelioScope, an Aurora Inc. Company: "The Big Book of Solar Software Must-Haves"
Landing Page
Downlad des "Buches", 20 Seiten (Archiv)
Aus den "Must-Haves" folgt, dass man das kommerzielle Tool HelioScope kaufen muss. Trotzdem informativ.
Bei der Visualisierung muss abgestimmt werden, wo eine Anzeige zu PV-Anlage gut sichtbar angebracht werden soll. Welche Parameter sollen angezeigt werden? Welches Display wird dafür benötigt?
Beim Konzept 3. "Messung der Globalstrahlung an der Anlage" muss der Sensor zur Messung der Globalstrahlung eingekauft werden. Weiter sollte die momentane Leistung der Anlage angezeigt werden können. Evtl. soll die gemessene Globalstrahlung von einem Datenlogger addiert werden zur Strahlungssumme.
Beim Konzept 6. "Berechnung der Globalstrahlung an einem wolkenlosen Tag" sollte die momentane Leistung der Anlage angezeigt werden können. Notfall könnte die Leistung aber auch über einen Zähler ermittelt werden nach P = E/ΔT. Wird z.B. in 6 Minuten 0,6 kW eingespeist, dann ist das eine Leistung von 0,6 kWh /0,1 h = 6 kW.
Je nach Sonnenstand liefert die Anlage auch an einem wolkenlosen Tag unterschiedliche Leistung. Daher ist die Kenntnis der Kennlinie des Wechselrichters erforderlich (siehe oben). Das Rechnen mit einem festen Umwandlungswirkungsgrad, ηINV,conv = ηEU ist als Vereinfachung möglich. Abhängig insbesondere von der Temperatur der Module muss der Temperatur- und Globalstrahlungswirkungsgrad, ηMOD,T,G berechnet werden. Dazu müssen Werte aus dem Moduldatenblatt zur Temperaturkorrektur herangezogen werden. Ohne eine Temperaturkorrektur funktioniert das Verfahren nicht!
Eines von vielen anderen Verfahren zur Berechnung der momentanen Globalstrahlung ist das Bird-Model (1981) mit Excel-Datei (Download) und Paper.
Monitoringkonzept 6: Darstellung an einer konkreten PV-Anlage

PV-Anlage mit 2,04 kWp, 15,8 m2, Neigungswinkel 25°, Azimut -22°,
17 Solarmodule Kyocera KC 120-1 (polykristallin), Wechselrichter SMA Sunny Boy SWR 2000 (transformatorlos),
Netzteilmodem SWR-COM, Inbetriebnahme 2001, Investition 30931 DM oder 15815 EUR, 7752 EUR/kWp(!),
PV*SOL: Performance Ratio 78 %, spez. Jahresertrag 852 kWh/kWp.
Monitoringkonzept zur Solaranlage.
Messwertaufnahme mit Sunny Data am 11.07.2001, 13:15. 72 Betriebsstunden nach Inbetriebnahme. Modultemperatur 24 °C, separat gemessen.
Die ganz neue Anlage hat noch nicht einmal eine anfängliche Degradation.
Die PV-Module liefern 264 V ·8,382 A = 2213 W bei 2040 Wp – also 8,5 % mehr als unter STC!
Am Ausgang werden 2013 W gemessen. Der Anlagenwirkungsgrad oder Performance Ratio, PR = 2013/2213 = 91 %.
Dies ist viel mehr als der über das ganze Jahr gemittelt und von PV*SOL errechnete Wert von PR = 78 %.
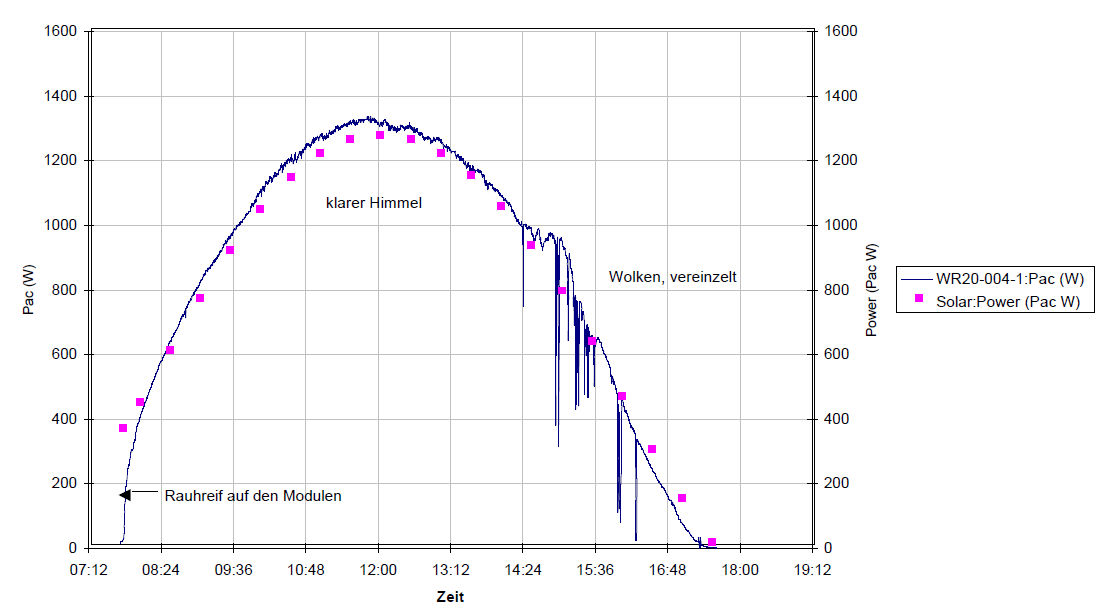
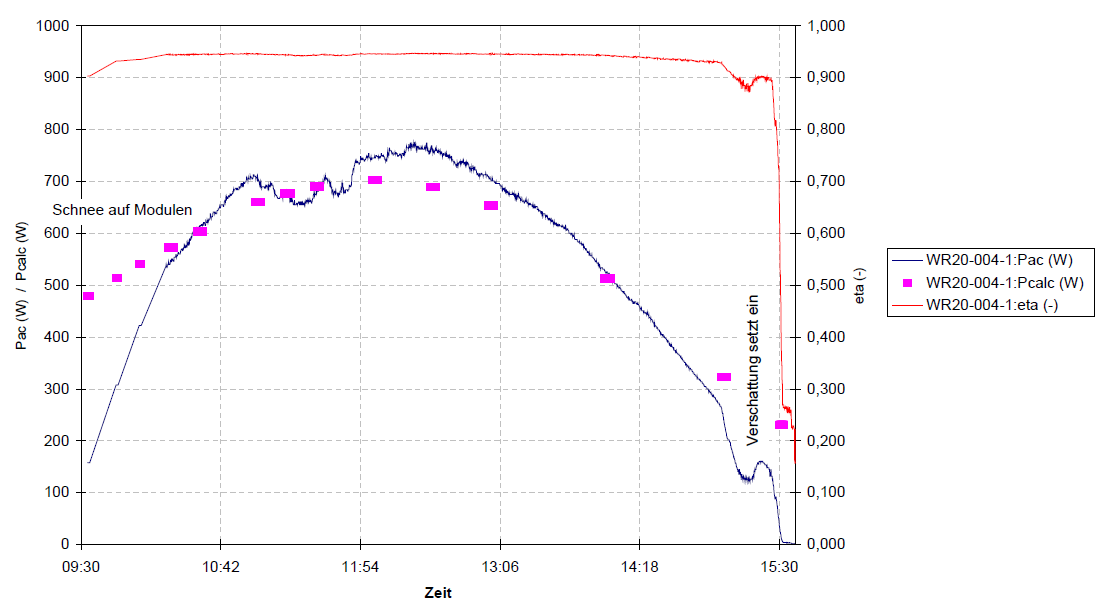
Die Leistung der PV-Anlage, PAC wird an einem weitgehend wolkenlosen Tag gemessen und aufgezeichnet (blaue Kurve).
Für ausgewählte Zeitpunkte wird die Globalstrahlung, Gc berechnet.
Daraus wird die Leistung der PV-Anlage berechnet, Pcalc (lila Punkte) und mit der Leistungsaufzeichnung verglichen.
Die rote Kurve zeigt den Wirkungsgrad des Wechselrichters, ηWR von bis zu 95 %.
Links: 2004-03-04, rechts: 2009-01-02.
Monitoringkonzept 6: Verallgemeinerung
Zur Bestimmung der momentanen Leistung der Anlage, PAC gibt es zwei Möglichkeiten:
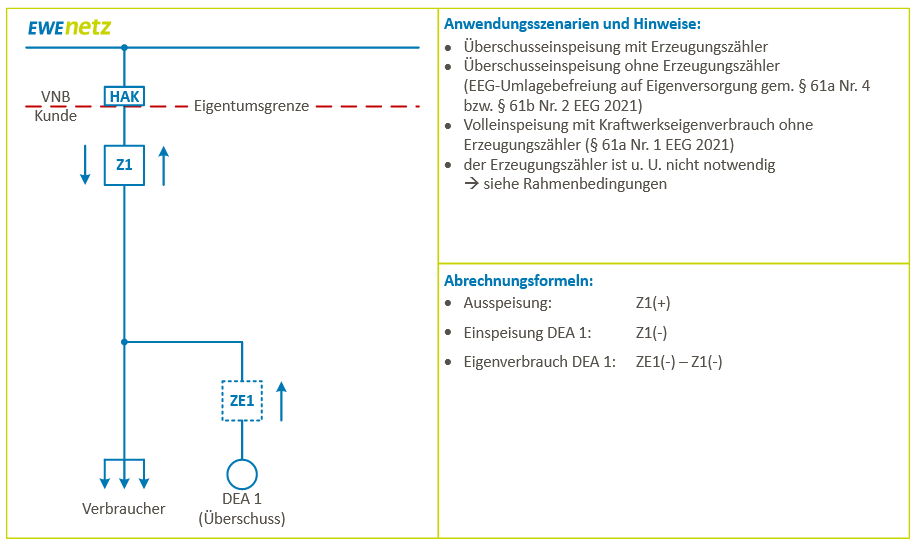
Zur Bestimmung der momentanen Temperatur der Module gibt es zwei Möglichkeiten:
Starte die DVD mit ...
user: PV Passwort: Die Abkürzung für "Bürgersolarkraftwerke" (in Versalien)
 Auslegung einer PV-Anlage durch Ermittlung der Anlagengröße – Eigenverbrauch und Überschusseinspeisung
Auslegung einer PV-Anlage durch Ermittlung der Anlagengröße – Eigenverbrauch und Überschusseinspeisung
 Kopfrechenverfahren für PV-Projekte
Kopfrechenverfahren für PV-Projekte
 Prof. Dr. Scholz
Prof. Dr. Scholz
 Aircraft Design and Systems Group (AERO)
Aircraft Design and Systems Group (AERO)
 Studiengang Flugzeugbau
Studiengang Flugzeugbau
 Fakultät Luftfahrt- und Fahrzeugsysteme
Fakultät Luftfahrt- und Fahrzeugsysteme
 HAW Hamburg
HAW Hamburg