Logo Landing Page Logo HAW Hamburg

Die Genauigkeit einer vereinfachten Berechnung der Steigzeit von Flugzeugen

Marcel Mutschall

Abstract
Ziel – Die Zeit die ein Flugzeug benötigt, um auf eine bestimmte Höhe zu steigen (die Steigzeit) kann mit einer Formel berechnet werden, die vereinfachend annimmt, dass die Steiggeschwindigkeit über dem gesamten Steigflug mit zunehmender Höhe linear abnimmt. Ziel der Untersuchung ist, zu ermitteln, ob die Annahme einer linear abnehmenden Steiggeschwindigkeit realistisch ist bzw. welche Fehler sich aus der Annahme ergeben. ----- Methode – Mit der Höhe ändern sich Parameter wie Luftdichte, Widerstand, Schub und damit auch die optimale Fluggeschwindigkeit für den Steigflug. Die Parameter beeinflussen sich dabei gegenseitig. Der Schub wird dabei nach drei unterschiedlichen Methoden berechnet, gegeben von Bräunling, Scholz und Howe. Analysiert wird der Verlauf des Schubes mit der Höhe und der Verlauf der Steiggeschwindigkeit mit der Höhe für jede der drei Schubberechnungen. Abschließend wird für jede Schubberechnung die Steigzeit verglichen wie sie sich ergibt a) aus der einfachen Formel und b) aus einer Integrationsberechnung, bei der der Verlauf der Steiggeschwindigkeit durch eine Funktion beschrieben wird. ----- Ergebnisse – Die drei Schubberechnungen liefern ausgehend vom gleichen Startschub unterschiedliche Schübe in der Höhe. In die Methode nach Bräunling gehen mehr Parameter ein als in die anderen beiden Methoden. Es kann angenommen werden, dass die Methode nach Bräunling genauer ist, der Beweis kann aber nicht geführt werden. Der Schub nach Scholz und Howe fällt nahezu linear mit der Höhe ab. Der Schubverlauf nach Bräunling zeigt eine deutliche Nichtlinearität. Es wird die Steigzeit von 0 km auf 11 km Höhe berechnet nach a) und b), mit jeder der drei Schubberechnungen. Dabei wird jeweils der Unterschied in der Steigzeit ermittelt. Aufgrund der Nichtlinearität im Schubverlauf zeigt die Methode nach Bräunling dann auch den größten Unterschied zwischen den Berechnungsmethoden von 7,1 %. Bei einer Schubberechnung nach Scholz ergeben sich 1,7 % und nach Howe 1,4 %. Wenn bereits zu Beginn Vereinfachungen, z.B. bezüglich des Triebwerksschubes, vorgenommen wurden, ist es in Hinblick auf den Aufwand und die zu erreicheneden Ergebnisse möglich, und zum Teil sinnvoll, die Berechnungen der Steigzeit mittels linearer Abnahme der vertikalen Geschwindigkeit durchzuführen. Es wird ausdrücklich darauf hingewiesen, dass es hier um den Vergleich von zwei Methoden zur Berechnung der Steigzeit geht und nicht um die Bewertung von Methoden zur Schubberechnung (für die keine Vergleichswerte vorlagen). ----- Praktischer Nutzen – Es konnte festgestellt werden, dass eine einfache Formel zur Berechnung der Steigzeit mit geringem Fehler angewandt werden kann – insbesondere wenn Methoden zur Schubberechnung vorliegen, bei denen der Schub annähernd linear mit der Höhe abnimmt. Bei großem Aufwand und realitätsnaher Betrachtung, z.B. nach Bräunling, führt der lineare Ansatz jedoch zu einem zu großen Fehler. Hierfür sollte die Berechnung der Steigzeit mittels Integration durchgeführt werden.

Download full text: PDF/A TextMutschall.pdf    Size:  9.6M
Date:2018-02-28
Type of work: Project
Advisor / Examiner:Dieter Scholz
Published by:Aircraft Design and Systems Group (AERO), Department of Automotive and Aeronautical Engineering, Hamburg University of Applied Sciences
This work is part of:transparent pin for text alignment Digital Library - Projects & Theses - Prof. Dr. Scholz --- http://library.ProfScholz.de pin
 
PERSISTENT IDENTIFIER:
URN: http://nbn-resolving.org/urn:nbn:de:gbv:18302-aero2018-02-28.018
DOI:http://doi.org/10.15488/4307
ARK:https://n2t.net/ark:/13960/t4vj31h1x
Associated research data:http://doi.org/10.7910/DVN/MX3K1B    (Program and Aircraft Data)
URLs registered with URN: Show all links associated with this work!
 
CATALOG ENTRY:
DNB: http://d-nb.info/1175497711
DataCite: Check inclusion of this title in DataCite!
Google Scholar: Check inclusion of this title in Google Scholar!
OpenAIRE: Check inclusion of this title in OpenAIRE!
BASE: Check inclusion of this title in BASE!
CORE: Check inclusion of this title in CORE!
Google: Check inclusion of this title in Google!
 
Keywords, German (GND): Luftfahrt,   Luftfahrzeug,   Flugmechanik,   Flugtriebwerk
Keywords, English (LCSH): Aeronautics,   Airplanes,   Airplanes--Performance,   Airplanes--Turbojet engines
Keywords, free: Flugzeug, Steigflug, Flugleistung, Strahltriebwerk, Schub, aircraft, flight, mechanics, flight mechanics, jet engine, thrust, climb
DDC: 629.13,    629.1341,    629.1333,    629.132
RVK: ZO 7250

© This work is protected by copyright

The work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License
CC BY-NC-SA
http://creativecommons.org/licenses/by-nc-sa/4.0

CC-BY-NC-SA

Any further request may be directed to:
Prof. Dr.-Ing. Dieter Scholz, MSME
E-Mail see: http://www.ProfScholz.de

Share this text:
Twitter LinkedIn Facebook XING Mendeley CiteULike InternetArchive E-Mail

Print Friendly and PDF

Quote this text:
ISO 690:
MUTSCHALL, Marcel, 2018. Die Genauigkeit einer vereinfachten Berechnung der Steigzeit von Flugzeugen. Project. Hamburg University of Applied Sciences, Aircraft Design and Systems Group (AERO). Available from: http://nbn-resolving.org/urn:nbn:de:gbv:18302-aero2018-02-28.018 [viewed JJJJ-MM-DD].
DIN 1505:
MUTSCHALL, Marcel: Die Genauigkeit einer vereinfachten Berechnung der Steigzeit von Flugzeugen. Hamburg University of Applied Sciences, Aircraft Design and Systems Group (AERO), Project, 2018. - URL: http://nbn-resolving.org/urn:nbn:de:gbv:18302-aero2018-02-28.018 (JJJJ-MM-DD)

Major results / graphical abstract:
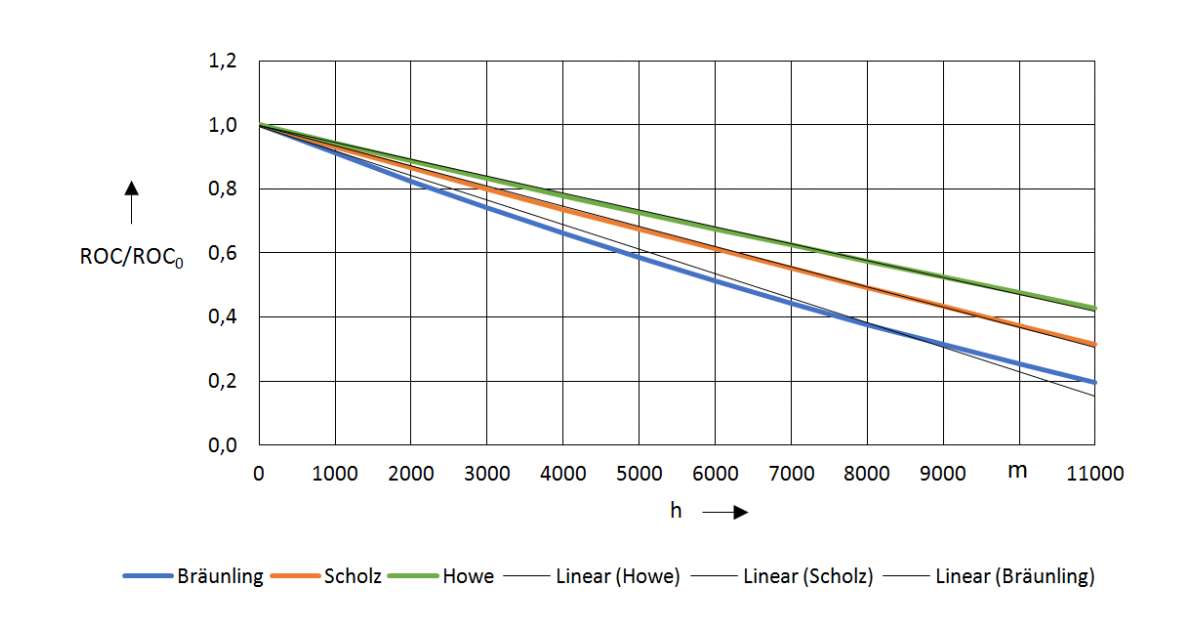
Major results / graphical abstract

Front page:
Cover Page

LAST UPDATE:  08 February 2019
AUTHOR:  Prof. Dr. Scholz
IMPRESSUM (PDF)

E-Mail-Address
home  Prof. Dr. Scholz
home  Aircraft Design and Systems Group (AERO)
home  Aeronautical Engineering   deutsch
home  Department of Automotive and Aeronautical Engineering  deutsch
home  Faculty of Engineering and Computer Science
home  Hamburg University of Applied Sciences